|
Figure 5.7: Coordinates for a pair of symmetric layers |
The constitutive equation for symmetric laminates (with 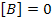 ) becomes ) becomes
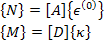 |
(5.46) |
The inverse constitutive relations can be given as
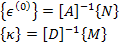 |
(5.47) |
This equation is consistent with Equation (5.39) through Equation (5.40). Setting 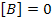 in Equation (5.40), we get in Equation (5.40), we get
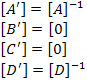 |
(5.48) |
Thus, we can write Equation (5.39) or Equation (5.47) as
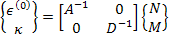 |
(5.49) |
Note: For symmetric laminates B matrix is zero. It means that there is no coupling between extension and bending action. Thus, the applied stresses will produce only in-plane and shear strains and it will not produce any curvatures. Thus, it is easy to understand that the mid-plane strains will be the strains in each ply.
Note: For symmetric laminates, the A and D matrices can be given as
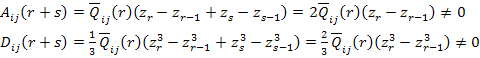 |
(5.50) |
For symmetric laminates, the uncoupling between extension and bending makes the analysis of laminates simpler. This is very useful because during thermal cooling down in the processing of such laminates there will not be any twisting due thermal loads.
|