Classification of Laminates:

In this section we are going to classify the laminates depending upon the stacking sequence nature. This classification is very helpful in the laminate analysis as some of the coupling terms become zero under specific laminate sequence and their arrangement with respect to the midplane.

Symmetric Laminates:

A laminate is called symmetric when the material, angle and thickness of the layers are the same above and below the mid-plane. For example laminate  is shown in Figure 5.6(a).
For symmetric laminates the matrix B is zero. This can be proved as follows:

Consider two layers r and s which have the same material, angle and thickness and are located symmetrically with respect to the mid-plane as shown in Figure 5.7. For these layers we can write the relation about the reduced stiffness matrix entries as

(5.28)

Figure 5.6: Classification of laminates examples (a) Symmetric laminate (b) Cross-ply laminate (c) Angle-ply laminate (d) Anti-symmetric laminate and (e) Balanced laminate The symmetry of location of these layers results in the following relation 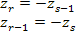(5.43) For these two layers, the contribution of to B matrix of the laminate is 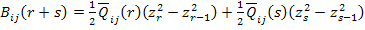(5.44) which upon substituting Equations (5.42) and (5.43) becomes 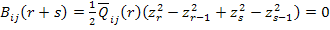(5.45) From this derivation it is very clear that the contribution of any pair of symmetric layers to B matrix is always zero. Thus, the B matrix is zero for symmetric laminates. However, one can show that the matrices A and D are not zero for symmetric laminates.