|
Specially Orthotropic Laminates:
The laminates for which the terms 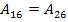 are zero are called specially orthotropic laminates. It is clear that such laminates do not show coupling between in-plane extensional and shear responses. are zero are called specially orthotropic laminates. It is clear that such laminates do not show coupling between in-plane extensional and shear responses.
Note that the cross-ply, angle-ply and anti-symmetric laminates are specially orthotropic laminates. These laminates by their design have 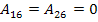 . For cross-ply laminates, the terms . For cross-ply laminates, the terms 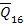 and and 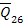 are identically zero. Hence, there is no restriction on the lamina thickness for cross-ply laminate to be a specially orthotropic laminate. However, for an angle ply and anti-symmetric laminates the thicknesses of a pair of are identically zero. Hence, there is no restriction on the lamina thickness for cross-ply laminate to be a specially orthotropic laminate. However, for an angle ply and anti-symmetric laminates the thicknesses of a pair of 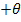 and and 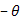 laminate should be same. laminate should be same.
Other specially orthotropic laminates includes the combination of cross-ply and angle ply laminates
.
For example,
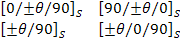 |
Quasi-Isotropic Laminates:
A laminate is called quasi-isotropic when its extensional stiffness matrix behaves like an isotropic material. This requires that 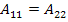 , , 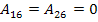 and and 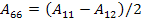 . Further, this extensional stiffness matrix is independent of orientation of layers in laminate. This requires a laminate with . Further, this extensional stiffness matrix is independent of orientation of layers in laminate. This requires a laminate with 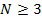 equal thickness layers and N equal angles between adjacent fibre orientations. The N equal angles, equal thickness layers and N equal angles between adjacent fibre orientations. The N equal angles, 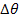 between the fibre orientations in this case can be given as between the fibre orientations in this case can be given as
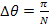 |
(5.53) |
The quasi-isotropic laminate with this construction for N=3, 4 and 6 will have fibre orientations as shown in Figure 5.8.
Figure 5.8: Fibre orientations in a typical quasi-isotropic laminates |
It should be noted that the isotropy in these laminates is in-plane only. The matrices B and D may not behave like an isotropic material. Hence, such laminates are quasi-isotropic in nature.
Some examples of quasi-isotropic laminate are: 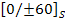 , , 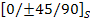 . .
|