|
Strain Displacements Relations:
The strain displacement relations for infinitesimal strains using the displacement field as in Equation (5.6) can be given as
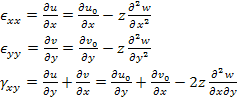 |
(5.12) |
The above equation can be written as
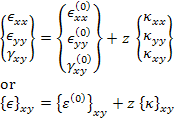 |
(5.13) |
where 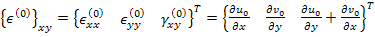 are the midplane strains and are the midplane strains and 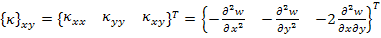 represents the midplane curvatures. The terms represents the midplane curvatures. The terms 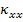 and and 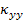 are the bending moment curvatures and are the bending moment curvatures and 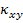 is the twisting moment curvature. is the twisting moment curvature.
Note: It is clear from Equation (5.6) and Equation (5.13) that the midplane strains 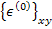 and the curvatures and the curvatures 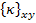 are independent of z location. are independent of z location.
Note: From Equation (5.13), we see that the strains are continuous through the thickness of laminate and they vary linearly.
State of Stress in a Laminate:
The stresses at any location can be calculated from the strains and lamina constitutive relations. It is assumed that the lamina properties are known. Hence, the constitutive equation for a kth lamina is known, that is, the reduced stiffness matrices (in principal material directions and global directions) are known. Thus, the stresses in kth lamina can be given as
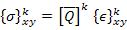 |
(5.14) |
Now, using Equation (5.13), we can write the stresses as
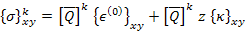 |
(5.15) |
In these equations, the strains are given at a z location where the stresses are required. It should be noted that the strains are continuous and vary linearly through the thickness. If we look at the stress distribution through the thickness it is clear that the stresses are not continuous through the thickness, because the stiffness is different for different laminae in thickness direction. In a lamina the stress varies linearly. The slope of this variation in a lamina depends upon its moduli. However, at the interface of two adjacent laminae there is a discontinuity in the stresses. The same thing is depicted in Figure 5.3 with three layers.
Figure 5.3: Elucidation of stress discontinuity at lamina interfaces in a laminate |
Note: The reduced transformed stiffness matrix 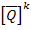 forkth lamina used in Equation (5.15) is the same as in the chapter on Planar Constitutive Equations. There we considered the state of stress as planar and the transverse normal strain was not zero. However, in this laminate theory we have plane stress assumption as well as all transverse strains are zero (plane strain conditions as well). Thus, we have an anomaly of transverse normal strains in using Equation (5.14). However, we will use this reduced transformed stiffness for a lamina. Inspite of this anomaly, the laminate theory works well (within its own scope). A detailed study on this issue can be seen in literature. However, this issue is out of scope of this course and will not be dealt with here. forkth lamina used in Equation (5.15) is the same as in the chapter on Planar Constitutive Equations. There we considered the state of stress as planar and the transverse normal strain was not zero. However, in this laminate theory we have plane stress assumption as well as all transverse strains are zero (plane strain conditions as well). Thus, we have an anomaly of transverse normal strains in using Equation (5.14). However, we will use this reduced transformed stiffness for a lamina. Inspite of this anomaly, the laminate theory works well (within its own scope). A detailed study on this issue can be seen in literature. However, this issue is out of scope of this course and will not be dealt with here. |