|
Displacement Field:
The strain-displacement field is derived using two approaches. In the first approach the deformation of the laminate according to the Kirchhoff - Love assumptions for bending and stretching is used. The undeformed and deformed geometries of laminate are used to develop the displacement field. In the second approach the transverse strain components resulting from the above assumptions are used. Further, using mathematical definitions of these strain components the displacement field is obtained. Thus, from this displacement field all strain components are obtained.
First Approach:
The Figure 5.2(a) shows the geometry of a laminate in undeformed configuration and Figure 5.2(b) shows the deformed geometry according to Kirchhoff-Love assumptions in xz plane. Any generic normal to the undeformed mid-plane remains normal to the deformed mid-plane. This assumption results in zero transverse shear strains, that is, . However, due to stretching action the point of intersection of midplane and a normal moves by a distance along x axis. Further, the same point moves by distance in z direction due to bending action. The second assumption that the normal to the mid-plane does not change in length requires that the transverse normal strain, that is, . This holds true when the transverse deflection of any point in the laminate is independent of z location, that is, it is a function of x and y only and a constant for a given x and y location. So, we can write
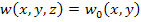 |
(5.1) |
Now, from the figure it is easy to find the slope of the deformed mid-plane as
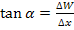 |
(5.2) |
Since, the deformations in this theory considered are very small, we can write
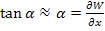 |
(5.3) |
Figure 5.2: Laminate geometry (a) undeformed and (b) deformed |
Now consider a generic point P on the mid-plane which is located at distance z from the mid-plane. After deformation, the displacement of this point along x direction can be given from the Figure 5.2 as
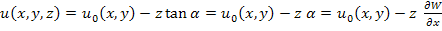 |
(5.4) |
Similarly, for the deformation in yz plane we can express the slope of the deformed mid-plane as . Thus, the displacement of a generic point along y axis can be given as
Thus, the complete displacement field for a generic point in the laminate according to the classical laminate theory is given below:
Note that the displacements 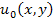 , , 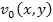 and and 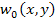 correspond to the mid-plane. Hence, they are called mid-plane displacements. correspond to the mid-plane. Hence, they are called mid-plane displacements.
Second Approach:
The second assumption is that the length of the normal to the mid-plane does not change even after deformation results into zero transverse normal strain. Thus,
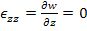 |
(5.7) |
Thus, from this expression it is clear that 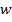 is a function of is a function of 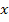 and and 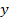 coordinates only. Thus, for any given location coordinates only. Thus, for any given location 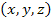 we can write the transverse deflection component as we can write the transverse deflection component as
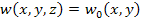 |
(5.8) |
From the first assumption of the Kirchhoff-Love theory that the normals remain straight and normal to mid-plane even after deformation, results into zero transverse shear strains. Thus, 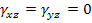 . .
Using the definitions of small strain, we can write the above equation as
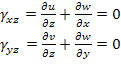 |
(5.9) |
From the first of the above equation we can write
Integrating this with respect to z, we get
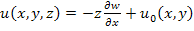 |
(5.10) |
where 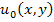 is a constant of integration which is function of x and y alone. Similarly, from the second of Equation (5.9), we can get is a constant of integration which is function of x and y alone. Similarly, from the second of Equation (5.9), we can get
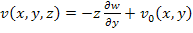 |
(5.11) |
Thus, Equations (5.8), (5.10) and (5.11) lead to the displacement field as in Equation (5.6). |