|
Inplane Resultant Forces:
The inplane forces per unit length are defined as
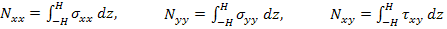 |
(5.16) |
Or these can be written as
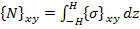 |
(5.17) |
Now, using Equation (5.15) we can write
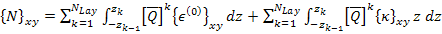 |
(5.18) |
Now recall that the midplane strains 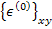 and the curvatures and the curvatures 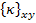 are independent of z location. The reduced transformed stiffness matrix are independent of z location. The reduced transformed stiffness matrix 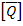 is function of thickness and constant over a given lamina thickness. Now we can replace the integration over the laminate thickness as sum of the integrations over individual lamina thicknesses. Thus, Equation (5.18) can be written as is function of thickness and constant over a given lamina thickness. Now we can replace the integration over the laminate thickness as sum of the integrations over individual lamina thicknesses. Thus, Equation (5.18) can be written as
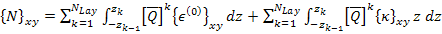 |
(5.19) |
Here, 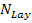 is the total number of layers in the laminate. This equation can be written as is the total number of layers in the laminate. This equation can be written as
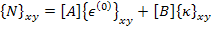 |
(5.20) |
where
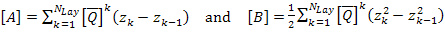 |
(5.21) |
The matrix 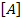 represents the in-plane stiffness, that is, it relates the in-plane forces with mid-plane strains and the matrix represents the in-plane stiffness, that is, it relates the in-plane forces with mid-plane strains and the matrix 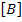 represents the bending stiffness coupling, that is, it relates the in-plane forces with mid-plane curvatures. represents the bending stiffness coupling, that is, it relates the in-plane forces with mid-plane curvatures.
It should be noted that the matrices 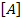 and and 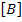 are symmetric as the matrix are symmetric as the matrix 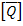 is also symmetric for each lamina in the laminate. is also symmetric for each lamina in the laminate.
The resultant in-plane forces are shown in Figure 5.4.
Figure 5.4: In plane resultant forces per unit length on a laminate
|
|