|
Transverse Modulus:
Consider an off-axis lamina subjected to in-plane transverse loading as shown in Figure 4.4. Thus, for this loading condition we have 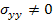 and and 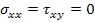 . .
Figure 4.4: Off axis lamina loaded in traction along y direction |
Let us define the transverse modulus as
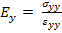 |
(4.69) |
Thus, from Equation (4.5) for the above loading, we can write
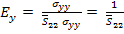 |
(4.70) |
If we express 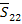 using engineering constants, we get using engineering constants, we get
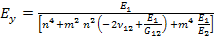 |
(4.71) |
From this expression, we can see that the modulus 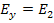 when when 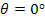 and and 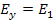 when when 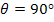 . The variation of the modulus . The variation of the modulus  with fibre orientation for AS4/3501-6 Epoxy material is shown in Figure 4.5. The variation of the modulus with fibre orientation for AS4/3501-6 Epoxy material is shown in Figure 4.5. The variation of the modulus  , similar to the variation of , similar to the variation of 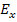 , for both positive and negative fibre orientations is identical in nature. Further, it can be observed that the curve for , for both positive and negative fibre orientations is identical in nature. Further, it can be observed that the curve for 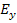 is shifted by is shifted by 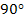 to that of to that of 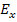 . .
Figure 4.5: Variation of transverse modulus with fibre orientation for AS4/3501-6 Epoxy |
Other Poisson’s Ratio:
The other Poisson’s ratio 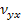 can be obtained from the loading condition given in Figure 4.4. Let us define this Poisson’s ratio as can be obtained from the loading condition given in Figure 4.4. Let us define this Poisson’s ratio as
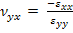 |
(4.72) |
Thus, using Equation (4.5) for this loading, it becomes
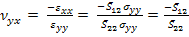 |
(4.73) |
which can be written using engineering constants as
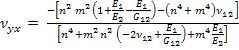 |
(4.74) |
The fibre orientation dependence of axial Poisson’s ratio and the other Poisson’s ratio for AS4/3501-6 Epoxy is shown in Figure 4.6.
Figure 4.6: Variation of Poisson's ratios with fibre orientation |
|