Axial Modulus:
Consider a unidirectional off axis lamina. This lamina is subjected to the loading 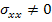 and and 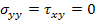 as shown in Figure 4.2. as shown in Figure 4.2.
Thus, from Equation (4.5) for this state of stress we can write the axial strain as
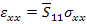 |
(4.61) |
The Young’s modulus in x-direction is now defined as
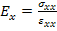 |
(4.62) |
Thus, from Equation (4.61), we can write
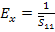 |
(4.63) |
Figure 4.2: Off axis lamina loaded in traction along x direction |
In the above equation, 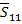 is written using compliance terms in principal material directions as is written using compliance terms in principal material directions as
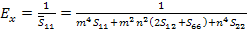 |
(4.64) |
Further, it can be writing compliance terms in principal directions using engineering constants doing some rearrangements as
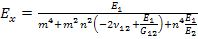 |
(4.65) |
From this expression it is easy to see that the modulus 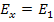 when when 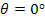 and and 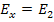 when when 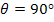 . The variation of the modulus . The variation of the modulus 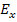 with fibre orientation for AS4/3501-6 Epoxy material is shown in Figure 4.3. The variation of the modulus with fibre orientation for AS4/3501-6 Epoxy material is shown in Figure 4.3. The variation of the modulus 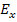 for both positive and negative fibre orientations is identical in nature. for both positive and negative fibre orientations is identical in nature.
Figure 4.3: Variation of axial modulus with fibre orientation for AS4/3501-6 Epoxy |
Axial Poisson’s Ratio:
The axial Poisson’s ratio 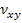 can also be obtained for above loading condition. This Poisson’s ratio is defined as can also be obtained for above loading condition. This Poisson’s ratio is defined as
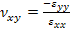 |
(4.66) |
Using Equation (4.61) we can write
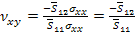 |
(4.67) |
Further, expressing the compliance terms in above equation in terms of engineering constants we can write
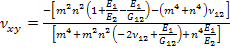 |
(4.68) |
|