|
In-plane Shear Modulus:
The in-plane or axial shear modulus for an off axis lamina can be obtained when it subjected to a pure shear loading as shown in Figure 4.7. Thus, for this loading condition we have 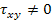 and . and .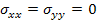 . .
For this loading, we define the in-plane shear modulus 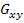 as as
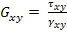 |
(4.75) |
With the help of Equation (4.5) we rewrite this equation as
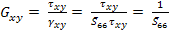 |
(4.76) |
And in terms of engineering constants, it becomes
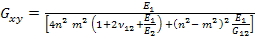 |
(4.77) |
The variation of 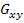 with fibre orientation between with fibre orientation between 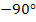 to to 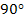 for AS4/3501-6 Epoxy material is shown in Figure 4.8. From this figure it can be seen that shear modulus is maximum when for AS4/3501-6 Epoxy material is shown in Figure 4.8. From this figure it can be seen that shear modulus is maximum when 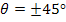 . At . At 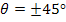 the value of shear modulus is the value of shear modulus is
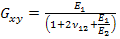 |
(4.78) |
Figure 4.7: Off axis lamina loaded in pure shear |
Note: When the material is isotropic, that is 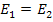 and and 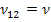 , then the above expression reduces to the familiar relation , then the above expression reduces to the familiar relation
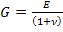 |
(4.79) |
The minimum value of shear modulus is seen when the lamina is loaded in shear in principal material directions and its value becomes
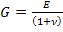 |
(4.80) |
Note: It is very important to note that the shear modulus of the lamina is a minimum when lamina is in principal directions and a maximum when fibre orientation is 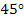 or or 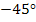 . Further, the behavior of a lamina under same pure shear for fibre orientation . Further, the behavior of a lamina under same pure shear for fibre orientation 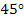 is significantly different from that of lamina with fibre orientation of is significantly different from that of lamina with fibre orientation of 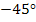 . The physical significance of this phenomenon is explained in greater details in the later section. . The physical significance of this phenomenon is explained in greater details in the later section.
Figure 4.8: Variation of shear modulus with fibre orientation for AS4/3501-6 |
|