|
2D Transformations about an Axis:
In planar stress condition we need to transform the stresses in plane. Let us write, similar to Equation (3.63), the transformation equation for stresses as
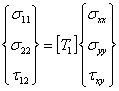 |
(4.32) |
where 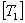 is the transformation matrix for stress tensor. For the above equation, using Equation (3.64), this matrix can be written as is the transformation matrix for stress tensor. For the above equation, using Equation (3.64), this matrix can be written as
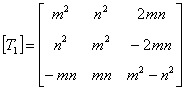 |
(4.33) |
Similarly, we can write the strain transformation equation in the following form.
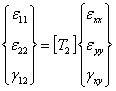 |
(4.34) |
where 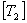 is the transformation matrix for strain tensor. We can find this matrix using Equation (3.69) and the above relations as is the transformation matrix for strain tensor. We can find this matrix using Equation (3.69) and the above relations as
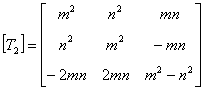 |
(4.35) |
Note: The transformation matrices 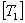 and and 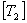 are not symmetric. There is a difference of factor 2 in two entries of these matrices. are not symmetric. There is a difference of factor 2 in two entries of these matrices.
Note: The transformation matrices 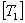 and and 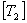 can be inverted using following relation can be inverted using following relation
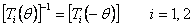 |
(4.36) |
The readers should verify this result.
Note: We have used the same matrix notation for stress and strain transformation matrices (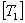 and and 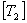 ) in 3D case and plane stress case. However, the readers should note the corresponding differences. ) in 3D case and plane stress case. However, the readers should note the corresponding differences.
|