|
Let us compare this equation with corresponding 3D equation (Eq. (4.12). It can easily be seen that the compliance terms of the constitutive equation are identical for 3D and plane stress problems. Thus, we can write for the plane stress problems as
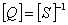 |
(4.25) |
It is easy to invert a 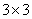 matrix. In fact, you need to invert a matrix. In fact, you need to invert a 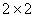 matrix. Thus, we can write the individual reduced stiffness entries in terms of compliance entries as matrix. Thus, we can write the individual reduced stiffness entries in terms of compliance entries as
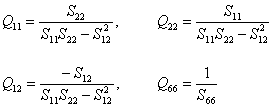 |
(4.26) |
Compliance and Stiffness Coefficients Using Engineering Constants
Let us write the compliance and stiffness matrices using engineering constants. It is easy to see that the individual entries of the compliance matrix in plane stress problem are same as the 3D compliance. Thus, we write for the plane stress problem the compliance entries as
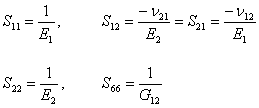 |
(4.27) |
Here, we have used the property that compliance matrix is symmetric, that is, 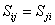 . Using . Using 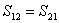 , we can develop the reciprocal relationship for 2D case as , we can develop the reciprocal relationship for 2D case as
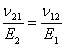 |
(4.28) |
Note: It is easy to see for a plane stress problem of an orthotropic material that only four of the five material constants are independent.
We can write the individual terms of reduced stiffness matrix in principal material directions by using Equation (4.26) and Equation (4.27) as
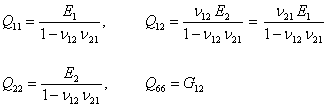 |
(4.29) |
Note: For a transversely isotropic material there is no reduction of the number of independent constants for plane stress problem.
One can write the constitutive equation in material coordinates, using Equation (3.42), Equation (3.43) and introducing the corresponding reduction in out of plane direction as
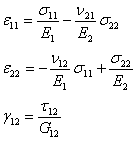 |
(4.30) |
It is easy to write the compliance coefficients in Equation (4.27) from these relations. Further, we can write the above relations in inverted form as
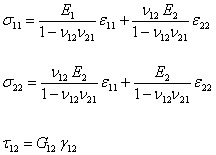 |
(4.31) |
These relations lead to individual reduced stiffness coefficients given in Equation (4.29).
|