Thus, the out of plane transverse shear strains are zero. Now, let us write the out of plane transverse normal strain using Equation (4.12) as
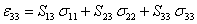 |
(4.15) |
Using and Equation (4.13) in the above equation, we get
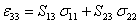 |
(4.16) |
and the inplane strain components are given as
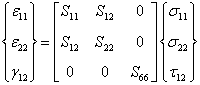 |
(4.17) |
This equation is called reduced constitutive equation using compliance matrix.
We have the 3D constitutive equation using stiffness matrix in principal material directions as (Equation . (3.26))
 |
(4.18 |
We have from the condition of plane stress problem that 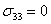 . Thus, using Equation. (4.18), we can write . Thus, using Equation. (4.18), we can write
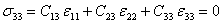 |
(4.19) |
This leads to non-zero transverse normal strain 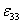 as as
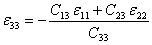 |
(4.20) |
Using Equation. (4.18), we can write the inplane stress components as
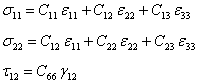 |
(4.21) |
Putting the expression for 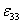 from Equation. (4.20) in above equation, we get from Equation. (4.20) in above equation, we get
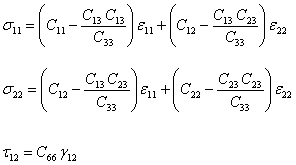 |
(4.22) |
This equation is written in matrix form as
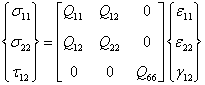 |
(4.23) |
where, the 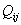 terms can be written using index notations as follows terms can be written using index notations as follows
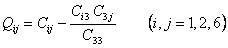 |
(4.24) |
Note: The reduced stiffness matrix is symmetric.
Note: The readers should again understand the difference between 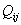 and and 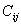 terms. They are not the same. terms. They are not the same.
The inversion of Equation (4.23) should give us Equation (4.17), that is,
|