|
Reduced Transformed Stiffness Matrix
The equation for in-plane components of stress in terms of the transformed stiffness coefficients is
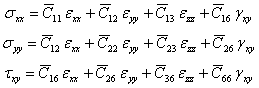 |
(4.8) |
Substituting 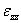 from Equation (4.7) into Equation (4.8) and upon simplification, we get from Equation (4.7) into Equation (4.8) and upon simplification, we get
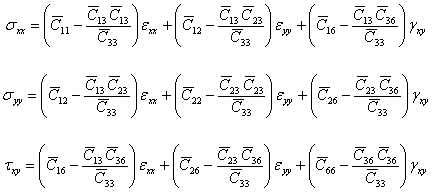 |
(4.9) |
The above equation is written in matrix form as
 |
(4.10) |
where the transformed reduced stiffness coefficients 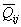 are defined as are defined as
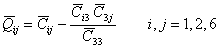 |
(4.11) |
Note: Transformed reduced stiffness matrix is symmetric.
Note: It is very important to note that the transformed reduced stiffness terms for plane stress, 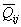 , are not simply the corresponding terms, , are not simply the corresponding terms, 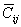 taken from the 3D stiffness matrix. This should be clear from the fact that the inverse of a taken from the 3D stiffness matrix. This should be clear from the fact that the inverse of a 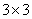 matrix is different from that of a matrix is different from that of a 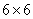 . This can easily be seen from Equation (4.11). The readers should easily understand that when . This can easily be seen from Equation (4.11). The readers should easily understand that when 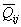 terms are used to define a constitutive equation, then it is a reduced transformed constitutive equation. terms are used to define a constitutive equation, then it is a reduced transformed constitutive equation.
Plane Stress for Orthotropic Material
Let us recall the constitutive equation for orthotropic material in principal directions.We can write the constitutive equation using compliance matrix as (Equation (3.45))
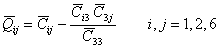 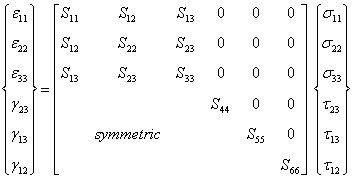 |
(4.12) |
We have planar state of stress for orthotropic lamina. Then we have out of plane transverse stress components zero, that is,
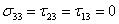 |
(4.13) |
Let us write the out of plane transverse shear strains using this information and Equation (4.12) as
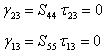 |
(4.14) |
|