Introduction
In the previous chapter, we have developed 3D constitutive equations. While analyzing composites, most of the times a planar state of stress actually exists. It is noted that a typical unidirectional lamina has very small thickness compared to its planar (xy) dimensions. Thus, it is appropriate to assume a planar state of stress in a lamina. In this chapter, we are going to derive a constitutive equation for plane stress problem in unidirectional laminar composite.
Plane Stress for Monoclinic (or Rotated Orthotropic) Material
3D constitutive equation for a single layer of a unidirectional composite with a fiber orientation 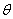 relative to the global coordinate is relative to the global coordinate is
 |
(4.1) |
For a state of plane stress, we have
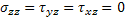 |
(4.2) |
Thus, it is easy to see that the two out of plane shear strains 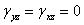 are zero. We can write these strains using Equation (4.1) as are zero. We can write these strains using Equation (4.1) as
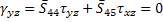 |
(4.3) |
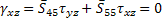 |
The out of plane normal strain 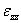 is expressed using Equation (4.1) and Equation (4.2) as is expressed using Equation (4.1) and Equation (4.2) as
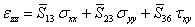 |
(4.4) |
Note that this strain component is not zero.
In plane components of strain for a plane stress state can be written using Equation (4.1) as
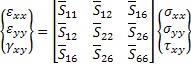 |
(4.5) |
From 3D constitutive equation (Equation (3.72)) for the transformed stiffness, we can write 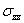 as as
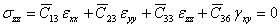 |
(4.6) |
From this equation, we can get the out of plane transverse normal strain as
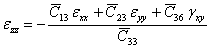 |
(4.7) |
Thus, the out of plane normal strain is expressed in terms of in-plane strain components and known stiffness coefficients. |