Lamina Constitutive Relations in Global Coordinates:
The plane stress constitutive equation in principal material coordinates is
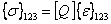 |
(4.37) |
Let us write the stresses and strains in terms of components in global directions using Equation (4.32) and Equation (4.34). The above equation can be re-written to give stresses in global coordinates as
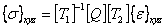 |
(4.38) |
We define the plane stress transformed reduced stiffness matrix 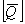 as as
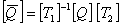 |
(4.39) |
Introducing this definition in Equation (4.38), we get
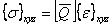 |
(4.40) |
The above equation is written in expanded form as
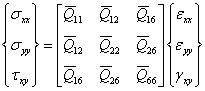 |
(4.41) |
Note: 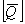 is a symmetric matrix. Further, it is a fully populated matrix with non zero is a symmetric matrix. Further, it is a fully populated matrix with non zero 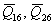 coefficients. coefficients.
Thus, using Equation (4.33), Equation (4.35 in Equation (4.39), we can write the individual terms in expanded form as
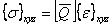  |
(4.42) |
Note: Reduced stiffness coefficients are fourth order in the sine and cosine functions.
Note: 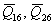 are very important. They define the coupling between in-plane normal and shear responses. Figure 4.1 shows response of an isotropic and orthotropic material under traction. The behaviour of an orthotropic lamina loaded along fibre direction and perpendicular to fibre direction is essentially similar to an isotropic material. However, for an off axis lamina, the behaviour clearly shows the coupling between normal and shear terms. are very important. They define the coupling between in-plane normal and shear responses. Figure 4.1 shows response of an isotropic and orthotropic material under traction. The behaviour of an orthotropic lamina loaded along fibre direction and perpendicular to fibre direction is essentially similar to an isotropic material. However, for an off axis lamina, the behaviour clearly shows the coupling between normal and shear terms.
Figure 4.1: Normal shear coupling in orthotropic lamina |
The transformed plane stress constitutive equation can also be given in inverted form of Equation (4.40) as
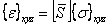 |
(4.43) |
where
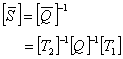 |
(4.44) |
Using 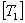 from Equation (4.33) and from Equation (4.33) and 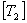 from Equation (4.35) in the above equation, we get the individual coefficients of transformed reduced compliance matrix as from Equation (4.35) in the above equation, we get the individual coefficients of transformed reduced compliance matrix as
 |
(4.45) |
Note: The same notation has been used for compliance matrices in principal directions 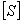 and transformed directions and transformed directions 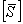 in 2D and 3D. This is because the corresponding terms are identical. However, for the stiffness coefficients these are different in 2D and 3D. in 2D and 3D. This is because the corresponding terms are identical. However, for the stiffness coefficients these are different in 2D and 3D.
Note: One can see the difference between the stiffness values by algebra involved. The inverse of the 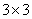 compliance matrix for plane stress case is different from the inverse of the compliance matrix for plane stress case is different from the inverse of the 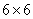 matrix for 3D case. matrix for 3D case.
|