Thermal Effects:
Thermal effects (effects due to change in temperature) are very important in composite materials for various reasons. The analysis of composites with thermal effects and effective thermal properties of the composite are two of the main reasons.
Important issues from analysis point of view:
- The composite materials are used in environment where thermal gradients are unavoidable. For example, the helicopter containing composite fuselage operates at -50° C during winter at Leh and same helicopter can operate at +50° C during summer in the desert of Rajasthan. Thus, the effect of temperature gradient on the service performance of the composite is very important. In such service conditions, the layers of composite material tend to expand or contract but are restricted due to adjacent layers. Thus, it induces thermal stresses.
- Most of the fabrication processes of polymer matrix composites have thermal cycles for matrix curing. A typical cycle involves raising the temperature to a certain level and holding it there for specified time and bringing it back to room temperature. It is well known that the fibre and matrix materials have different coefficients of thermal expansion (defined below). This mismatch produces residual thermal stresses because the fibres and matrix material are constrained in a composite.
Important issues from effective thermal properties point of view:
The second reason for the study of thermal effects is the effective properties of the composite materials.
- Finding effective thermal properties of the composite theoretically to get an estimate requires sophisticated mathematical modeling when one considers:
- Difference in coefficients of thermal expansion of fibre and matrix materials
- The direction dependence of coefficients of thermal expansion in these materials
- Curing cycle temperature variations. This point is important because for some of the materials the coefficient of thermal expansion changes with temperature.
- Finding the effective thermal properties for lamina in global direction with oriented fibres as shown in Figure 3.9 requires a special attention.
Further, finding these effective properties by laboratory test is also a challenge. Thus, for the various reasons mentioned above the study of thermal effect is very important. In the following, we develop a systematic way to handle effective thermal properties of a lamina along global directions.
It is well known that when a material is subjected to thermal gradient, it undergoes a deformation. The strain due to thermal changes is called thermal strain (denoted by superscript (T)). In general, the thermal strain is proportional to the temperature change 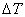 . The constant of proportionality is called coefficient of thermal expansion. Thus, we can write the thermal strains in principal material directions for an orthotropic material as . The constant of proportionality is called coefficient of thermal expansion. Thus, we can write the thermal strains in principal material directions for an orthotropic material as
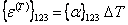 |
(3.83) |
where 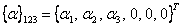 denote the coefficients of thermal expansion in principal material directions. It should be noted that for an orthotropic material in principal directions there are no shear strains due to thermal effects like in an isotropic material. For an isotropic material the coefficient of thermal expansion is same in any direction. However, for an orthotropic material denote the coefficients of thermal expansion in principal material directions. It should be noted that for an orthotropic material in principal directions there are no shear strains due to thermal effects like in an isotropic material. For an isotropic material the coefficient of thermal expansion is same in any direction. However, for an orthotropic material 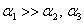 . The thermal expansion of an elemental cube in principal directions for an isotropic and orthotropic material is shown in Figure 3.10. . The thermal expansion of an elemental cube in principal directions for an isotropic and orthotropic material is shown in Figure 3.10.
These thermal strains will not produce stresses unless these are constrained. The thermal strains which do not produce stresses are known as free thermal strains. However, in case of composites the fibres and matrix are constrained in a lamina and layers are constrained in a laminate. Thus, in composite the thermal strains produce the thermal stresses.
The thermal strains are given in principal material directions as given in Equation (3.83). Let us consider that we need to find these strains in a global coordinate system (refer Figure 3.9). We need to transform them from 123 coordinate system to xyz coordinate system by a rotation 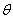 about 3-axis. Thus, similar to Equation (3.68), we can write about 3-axis. Thus, similar to Equation (3.68), we can write
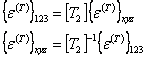 |
(3.84) |
Substituting Equation (3.83) in the above equation,
 |
(3.85) |
where
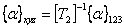 |
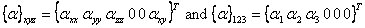 |
(3.86) |
Figure 3.10: Thermal expansion in an isotropic and orthotropic material |
On substitution of 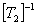 in the above equation, we get the following individual terms of coefficients thermal expansion in xyz directions. in the above equation, we get the following individual terms of coefficients thermal expansion in xyz directions.
 |
(3.87) |
Using Equation (3.87) in Equation (3.85), the engineering thermal strains in global coordinates are given as
 |
(3.88) |
Thus, from this equation it should be noted that the transformation of thermal strains in global coordinates gives normal strain components and a shear strain component in xy plane for an orthotropic material with 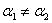 and fiber orientations other than and fiber orientations other than 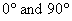 . .
|