Compliance Transformation:
We are going to follow a procedure to transform compliance matrix similar to one used for transformation of a stiffness matrix. We have the constitutive equation in principal material direction as in Equation (3.70). We can write this in inverted form as
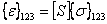 |
(3.77) |
using Equation (3.63) and Equation (3.68) we get
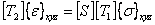 |
(3.78) |
Pre-multiplying both sides by 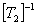 , we get , we get
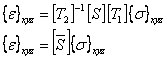 |
(3.79) |
where, we define the transformed compliance matrix 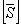 as
as
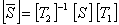 |
(3.80) |
Alternately, we can find 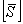 by inverting the transformed stiffness matrix by inverting the transformed stiffness matrix 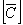 . Thus, inverting . Thus, inverting 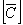 from Equation (3.73), we get from Equation (3.73), we get
After carrying out the calculation for 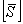 , it is easy to give its form as follows , it is easy to give its form as follows
 |
(3.81) |
Note that 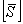 has the same symmetric form as the transformed stiffness matrix. has the same symmetric form as the transformed stiffness matrix.
The individual terms of the compliance matrix are obtained by carrying out multiplication of matrices as in Equation (3.82) and are given below.
 |
(3.82) |
|