Introduction
In the previous lecture we have derived the stiffness matrix in terms of engineering constants using the compliance relations. Further, we have seen the constraints over the engineering constants in orthotropic materials. Then we have visited the stress and strain transformation. In the present lecture we will see the stiffness and compliance transformation about an axis. Further, we will address the effect of thermal and hygroscopic actions on lamina constitutive equations.
Stiffness Transformation:
It is required to relate the stress components with strain components in global xyz directions. The stiffness matrix which relates the stress and strain components in global directions is called as transformed stiffness matrix. We will derive an expression for the transformed stiffness matrix as follows.
The constitutive equation in principal material coordinates, as given in Equation (3.11), is
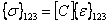 |
(3.70) |
Now, we express 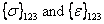 using Equation (3.63) to transform stresses and Equation (3.68) to transform strains. Substituting these equations, we get using Equation (3.63) to transform stresses and Equation (3.68) to transform strains. Substituting these equations, we get
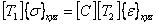 |
(3.71) |
Pre-multiplying both sides by 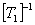 , we get , we get
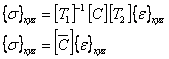 |
(3.72) |
where we define the transformed stiffness matrix  as as
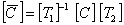 |
(3.73) |
The transformation matrices 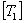 and and 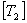 can be inverted as follows can be inverted as follows
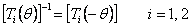 |
(3.74) |
The final form of the transformed stiffness matrix is given in Equation (3.75).
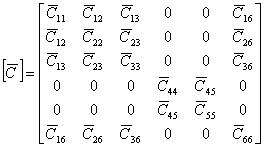 |
(3.75) |
The individual 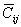 terms of this matrix are determined using terms of this matrix are determined using 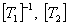 and relation for and relation for  . The individual terms are given in Equation (3.76). . The individual terms are given in Equation (3.76).
Note: The transformed stiffness matrix is symmetric in nature.
Note: The transformed stiffness matrix given in Equation (3.75) has exactly the same form as a stiffness matrix for a monoclinic material. Thus, we can conclude that a transformation through an arbitrary angle 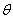 about direction 3, leads to a monoclinic material behaviour. about direction 3, leads to a monoclinic material behaviour.
The same can be seen from the plane of elastic symmetry considerations in xyz coordinate system. The given lamina is symmetric only about xy plane. Thus, the transformed stiffness matrix in Equation (3.75) is consistent with monoclinic material.
Note: Transformed stiffness coefficient terms are fourth order in the sine and cosine functions. It is very important to use appropriate precision level while calculating (in examinations and writing computer codes) these coefficients.
 |
(3.76) |
The constitutive equation 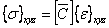 becomes becomes
|