Thermo-Elastic Constitutive Equation:

Let us assume that the total strain, 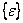 in a composite is a superposition of the free thermal strain  and the strain due to mechanical loads (also known as mechanical strains) . Thus,

Now, for mechanical strains we use the constitutive equation as

Thus, we can write the total thermo-elastic strain as

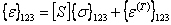(3.89)

Equation (3.89) can be written as

Premultiplying the above expression by 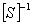, we get the stresses as

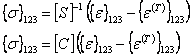(3.90)

Equation (3.90) is the basic constitutive equation for thermo-elastic stress analysis.

Using Equation (3.90) and similar to Equation (3.72) we can find the stresses due to thermo-elastic effects in global directions as,

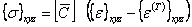(3.91)

where

Equation (3.91) is inverted to give the total strains in terms of the mechanical and free thermal strains as

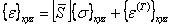(3.92)

Effect of Moisture:

The polymer matrix composite materials, during their service can absorb moisture from the environment. The effect of absorption of moisture is to degrade the various material properties of the composite. Further, this results in an expansion. It is called hygroscopic expansion. However, this expansion is again constrained as in thermal expansion. Hence, when dealing with the hygroscopic expansions, a treatment similar to thermal expansion is used.

The hygroscopic strains 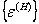 are assumed to be proportional to the percentage moisture absorbed, 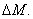 This percentage is measured in terms of weight of the moisture. The constant of proportionality, 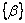 is the coefficient of hygroscopic expansion.

Thus, in principal coordinates the hygroscopic strains are

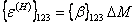(3.93)

 where

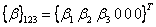(3.94)

denotes the coefficients of hygroscopic expansion in principal material directions. Following a similar procedure for thermal strains, we can write strains due to hygroscopic expansion in xyz coordinates as

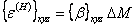(3.95)

We can write 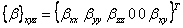 using values of in 123 directions as .

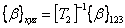Thus, comparing Equation (3.85) and Equation (3.95), it is easy to conclude that the coefficients of hygroscopic expansion will vary similar to the coefficients of thermal expansion as a function of orientation of fibres.