Strain Transformation:
In a similar way, we can transform the strain components from xy plane to 1-2 plane. In this transformation we will use engineering shear strains. Let us find the 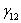 using the transformation equation similar to stress transformation and using strain symmetry as using the transformation equation similar to stress transformation and using strain symmetry as
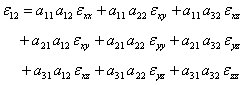 |
(3.65) |
Substituting the direction cosines and rearranging, we get
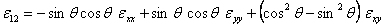 |
(3.66) |
We know from Equation (2.24) that the tensorial shear strains are half the engineering shear strains. Thus, in Equation (3.53) we substitute
On simplification and putting 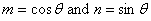 , we get , we get
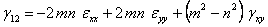 |
(3.67) |
The other five strain terms (using strain symmetry) on the left hand side are also obtained in a similar way. Let us write the final form of the relation as
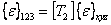 |
(3.68) |
Here, 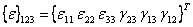 and and 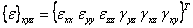 and and 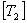 is the strain transformation matrix. Thus, comparing all the terms as in Equation (3.68), we can write is the strain transformation matrix. Thus, comparing all the terms as in Equation (3.68), we can write 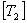 as as
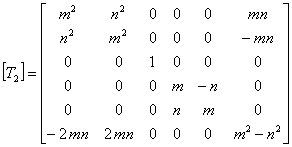 |
(3.69) |
Note: The transformation matrices, 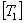 and and 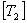 differ by factors 2 in two terms. differ by factors 2 in two terms.
Note: The transformation matrices, 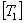 and and 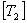 are not symmetric. are not symmetric.
Note: The order of stress and strain components in Equatjion (3.63) and Equation (3.68) is important. Some books and research articles follow different orders. The readers are cautioned to take a note of it.
|