Stress and Strain Transformation about an Axis
Often it is required to transform the stress or strain tensor from one coordinate axes system to another. For example, if the fibres in a lamina are not oriented along direction x, then we may need to transform the stress and strain components from principal material directions 1-2-3 to global directions xyz or vice-a-versa. It should be noted that the stress and strain tensors are second order tensors. Hence, they follow tensor transformation rules.
In this section we are going to introduce two notations. The subscripts 123 will denote a quantity (like constitutive equation, engineering constants, etc.) in principal material directions, while subscripts xyz will denote the corresponding quantity in global coordinate directions.
Figure 3.9: Unidirectional lamina with global xyz directions and principal material 1-2-3 directions |
Let us transform the stress and strain components for the case shown in Figure 3.9. Here, xy plane is rotated about direction z to 1-2 plane. Here, direction z and direction 3 are in same directions, that is, along the thickness direction of lamina. The direction cosines for this axes transformation are as given in Equation (2.2). However, these are again given below.
Stress Transformation:
Let us do the stress transformation as given in Equation (2.7). In this equation the primed stress components denote the component in 123 coordinate system. Using the expanded form of Equation (2.7) and stress symmetry, let us obtain 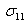 component of stress component of stress
Thus, substituting the values of direction cosines from above, we get
The remaining five stress terms (using stress symmetry) on the left hand side are also obtained in a similar way. Let us write the final form of the relation as
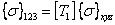 |
(3.63) |
Here, 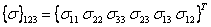 and and 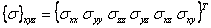 and and 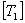 is the stress transformation matrix. Thus, comparing all the terms as in Equation (3.63), we can write is the stress transformation matrix. Thus, comparing all the terms as in Equation (3.63), we can write 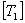 as as
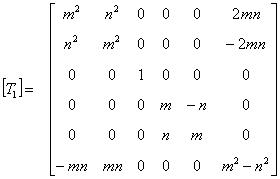 |
(3.64) |
where 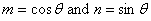 . It should be noted that . It should be noted that 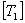 is not symmetric. is not symmetric.
|