Constraints on Engineering Constants in Orthotropic Materials
For orthotropic materials there are constraints on engineering constants. These constrains arise due to thermodynamic admissibility. For example, in case of isotropic materials it is well known that the Young’s modulus and shear modulus are always positive. Further, the Poisson’s ratio lager than half are not thermodynamically admissible. If these constrains are violated then it is possible to have a nonpositive strain energy for certain load conditions. However, for isotropic materials the strain energy must be a positive definite quantity.
In this section, based on the work done by Lempriere we are going to assess the implications of this thermodynamic requirement (positive definiteness of strain energy) for orthotropic materials.
The sum of work done by all stress components must be positive, otherwise energy will be created. This condition imposes a thermodynamic constraint on elastic constants. This condition requires that both compliance and stiffness matrices must be positive definite. In other words, the invariants of these matrices should be positive.
Let us look at this condition with physical arguments. For example, consider that only one normal stress component is applied. Then we can find the corresponding strain component from the corresponding diagonal entry of the compliance matrix. Thus, we can say that for the strain energy to be positive definite the diagonal entries of the compliance matrix must be positive. Thus,
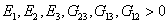 |
(3.53) |
In a similar way, it is possible under certain conditions to have a deformation which will give rise to only one normal strain component. We can find the corresponding stress using the corresponding diagonal entry in stiffness matrix. For the strain energy produced by this stress component to be positive the diagonal entry of the stiffness matrix must be positive. Thus, this condition reduces to
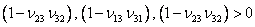 |
(3.54) |
and the determinant of the compliance matrix must also be positive. That is,
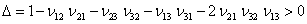 |
(3.55) |
Now, using the reciprocal relations given in Equation (3.49), the condition in Equation (3.54) can be expressed as
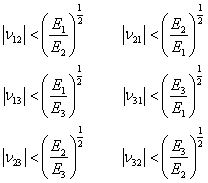 |
(3.56) |
This condition also justifies that the Poisson’s ratio greater than unity is feasible for orthotropic lamina. Poisson’s ratio greater than unity is sometimes observed in experiments.
The condition in Equation (3.55) can be written as
The terms inside the brackets are positive. Thus, we can write
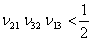 |
(3.57) |
This condition shows that all three Poisson’s ratios cannot have large positive values and that their product must be less than half. However, if one of them is negative no restriction is applied to remaining two ratios.
Let us consider the transverse isotropy as a special case. Let us consider transverse isotropy in 2-3 plane. Let
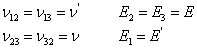 |
(3.58) |
Then, the conditions in Equation (3.56) reduce as
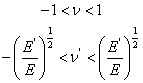 |
(3.59) |
and Equation (3.57) (using reciprocal relations in Eq. (3.49)) becomes as
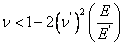 |
(3.60) |
The condition posed by above equation is more stringent than that posed in Equation (3.59). Note that the quantities 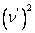 and and 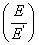 are both positive. Thus, the limits on Poisson’s ratio in transverse plane are are both positive. Thus, the limits on Poisson’s ratio in transverse plane are
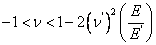 |
(3.61) |
Further, consider a special case of isotropic material where 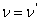 and and 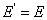 . This simplifies Equation (3.61) to a well known condition . This simplifies Equation (3.61) to a well known condition
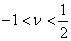 |
(3.62) |
|