The relations in Equation (3.47) or Equation (3.45) are referred to as the reciprocal relations. These relations are also written as
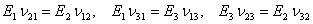 |
(3.49) |
It should be noted that, in general 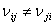 . From Equation (3.48) we can write for . From Equation (3.48) we can write for 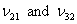 as as
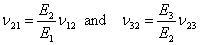 |
(3.50) |
It is known that for transversely isotropic material (in 2-3 plane) 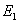 is much greater than is much greater than 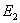 and and 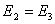 Thus, from the first of Equation (3.47) one can easily see that Thus, from the first of Equation (3.47) one can easily see that 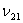 is much smaller than is much smaller than 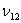 . Further, it is clear from the relation that . Further, it is clear from the relation that 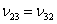 . .
Note: Since value of 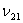 (and may be of other Poisson’s ratios) will be small, the readers are suggested to use appropriate precision level while calculating (in examinations and writing computer codes) any data involving these coefficients. (and may be of other Poisson’s ratios) will be small, the readers are suggested to use appropriate precision level while calculating (in examinations and writing computer codes) any data involving these coefficients.
We will get the stiffness matrix by inversion of compliance matrix. Equation (3.46) is substituted in Equation. (3.45) and the resulting equation is inverted to give the stiffness matrix of an orthotropic material as
 |
(3.51) |
where
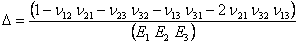 |
(3.52) |
is the determinant of stiffness matrix in Equation (3.51). We can write the stiffness matrix for transversely isotropic material with the following substitutions in the stiffness matrix.
Further, from the resulting, one can reduce the constitutive equation for isotropic material with following substitutions:
The readers should verify these results.
|