Constitutive Equation for an Orthotropic Material:
Now, let us assume that we have measured all the engineering constants of an orthotropic material along principal directions. With these engineering constants we know the relation between the strain and stress components as given in Equation (3.42) and Equation (3.43). Thus, it is easy to see that we can relate the strain components to stress components through compliance matrix. Let us recall from previous lecture the stiffness matrix for orthotropic material (Equation (3.26)). The inverse of this matrix (compliance) will have the same form as the stiffness matrix. Thus, we write the relationship between strain and stress components using compliance matrix as follows
Figure 3.8: Experiments to extract engineering constants for a transversely isotropic material |
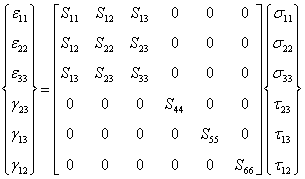 |
(3.45) |
Now compare Equation (3.42) and Equation (3.43) with Equation (3.45). This gives us the compliance coefficients in terms of engineering constants. The coefficients are given in Equation (3.46).
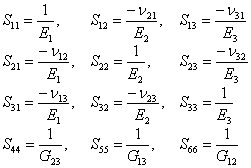 |
(3.46) |
It should be noted that like stiffness matrix, the compliance matrix is also symmetric. The compliance matrix given in Equation (3.45) is shown symmetric.
Note: It is known from our elementary knowledge of linear algebra that inverse of a symmetric matrix is also a symmetric matrix. Since, the stiffness matrix, which is the inverse of compliance matrix, is symmetric; the compliance matrix has to be symmetric.
Now, let us derive some more useful relations using the symmetry of compliance matrix. If we compare 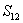 and and 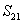 we get we get 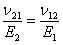 . Similarly, comparison of . Similarly, comparison of 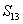 and and 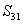 and comparison of and comparison of 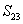 and and 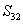 give two more similar relations. All these relations are given in Equation (3.47). give two more similar relations. All these relations are given in Equation (3.47).
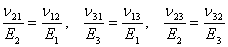 |
(3.47) |
or one can write this relation in index form as
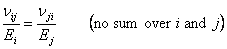 |
(3.48) |
|