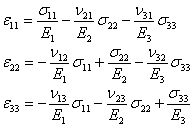 |
(3.42) |
whereas the engineering shear strain components are given as
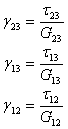 |
(3.43) |
Here, 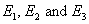 are the Young’s moduli in 1, 2 and 3 directions, respectively. Thus, are the Young’s moduli in 1, 2 and 3 directions, respectively. Thus, 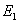 represents the axial modulus and represents the axial modulus and 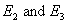 represent in-plane transverse and out-of-plane transverse moduli, respectively. Note that axial direction is along the fibre direction. represent in-plane transverse and out-of-plane transverse moduli, respectively. Note that axial direction is along the fibre direction.
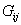 represents the shear moduli. G12,G13 are the axial shear moduli in two orthogonal planes that contain the fibers.G23 represents out-of-plane transverse shear modulus. Further, it should be noted that represents the shear moduli. G12,G13 are the axial shear moduli in two orthogonal planes that contain the fibers.G23 represents out-of-plane transverse shear modulus. Further, it should be noted that 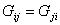 . .
The term 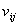 represents the Poisson’s ratio. It is defined as follows represents the Poisson’s ratio. It is defined as follows
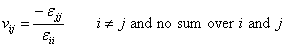 |
(3.44) |
where 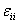 represents the strain in the direction of applied stress and represents the strain in the direction of applied stress and 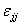 represents the strain the associated lateral direction. It should be noted that, in general represents the strain the associated lateral direction. It should be noted that, in general 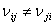 . .
We will mimic some (thought) experiments that we actually do in laboratory to extract these engineering constants. For example, we find engineering constants of a transversely isotropic lamina.
Experiment 1: The lamina is loaded in traction along the axial direction as shown in Figure 3.8 (a) and the strains in along three principal directions are recorded as the load is varied. The slope of the axial stress versus axial strain curve yields the axial Young’s modulus 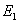 . The ratios . The ratios 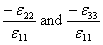 give the Poisson’s ratios give the Poisson’s ratios 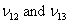 respectively. respectively.
Experiment 2: The lamina is loaded in traction along direction 2. The two views of this loading case are shown in Figure 3.8 (b). The slope of stress-strain curve in direction 2 gives the in-plane transverse Young’s modulus 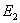 . Since, the material is isotropic in 2-3 plane, . Since, the material is isotropic in 2-3 plane, 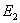 is also equal is also equal 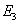 . The strains in all three directions are measured. The ratios . The strains in all three directions are measured. The ratios 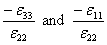 give the Poisson’s ratios give the Poisson’s ratios 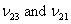 , respectively. , respectively.
Experiment 3: The lamina is loaded in shear in plane 1-2 as shown in Figure 3.8 (c). The slope of the in-plane shear stress and engineering shear strain curve gives the shear modulus 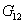 . Please note that if we load the lamina in 1-3 plane by shear then also we will get this modulus because the behaviour of material in shear in these two planes is identical. Thus, by shear loading in plane 1-2 gives . Please note that if we load the lamina in 1-3 plane by shear then also we will get this modulus because the behaviour of material in shear in these two planes is identical. Thus, by shear loading in plane 1-2 gives 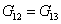 . .
Experiment 4: The lamina is loaded in shear in 2-3 plane as shown in Figure 3.8(d). The corresponding shear stress and engineering shear strain curve yields the shear modulus 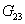 . .
Note: We will see the experimental details to measure some of these engineering constants in a chapter on experimental characterization of lamina, laminates, fibres and matrix materials. |