Strain Energy Density Function (W):

The strain energy density function W is given as

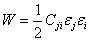(3.7)

with the property that

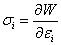(3.8)

It is seen that W is a quadratic function of strain. A material with the existence of W with property in Equation (3.8) is called as Hyperelastic Material.

                The W can also be written as

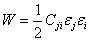(3.9)

Subtracting Equation (3.9) from Equation (3.7) we get

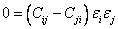(3.10)

which leads to the identity 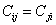. Thus, the stiffness matrix is symmetric. This symmetric matrix has 21 independent elastic constants. The stiffness matrix is given as follows:

(3.11)

The existence of the function W is based upon the first and second law of thermodynamics. Further, it should be noted that this function is positive definite. Also, the function W is an invariant (An invariant is a quantity which is independent of change of reference).

The material with 21 independent elastic constants is called Anisotropic or Aelotropic Material.
Further reduction in the number of independent elastic constants can be obtained with the use of planes of material symmetry as follows.

Material Symmetry:

It should be recalled that both the stress and strain tensor follow the transformation rule and so does the stiffness tensor. The transformation rule for these quantities (as given in Equation (3.1)) is known as follows

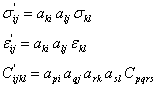(3.12)

where 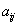are the direction cosines from i to j coordinate system. The prime indicates the quantity in new coordinate system.

When the function W given in Equation (3.9) is expanded using the contracted notations for strains and elastic constants given in Equation (3.11) W has the following form:

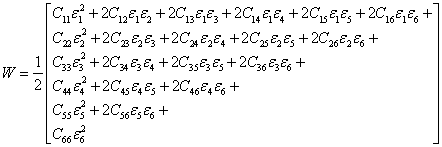(3.13)

Thus, from Equation (3.13) it can be said that the function W has the following form in terms of strain components:

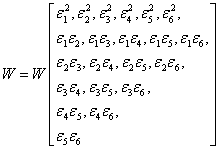(3.14)