(A) Symmetry with respect to a Plane:

Let us assume that the anisotropic material has only one plane of material symmetry. A material with one plane of material symmetry is called Monoclinic Material.
Let us consider the x₁- x₂ ( x₃= 0) plane as the plane of material symmetry. This is shown in Figure 3.1. This symmetry can be formulated with the change of axes as follows

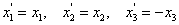(3.15)

With this change of axes,

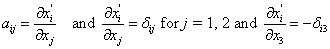(3.16)

This gives us along with the use of the second of Equation (3.12)

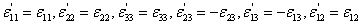(3.17)

First Approach: Invariance Approach

Now, the function W can be expressed in terms of the strain components 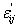. If W is to be invariant, then it must be of the form

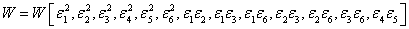(3.18)

Comparing this with Equation (3.13) it is easy to conclude that

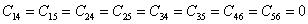(3.19)

Thus, for the monoclinic materials the number of independent constants are 13. With this reduction of number of independent elastic constants the stiffness matrix is given as

(3.20)