Introduction
In this lecture, we are going to develop the 3D constitutive equations. We will start with the the generalized Hooke’s law for a material, that is, material is generally anisotropic in nature. Finally, we will derive the constitutive equation for isotropic material, with which the readers are very familiar. The journey for constitutive equation from anisotropic to isotropic material is very interesting and will use most of the concepts that we have learnt in earlier Lecture 9.
The generalized Hooke’s law for a material is given as
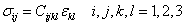 |
(3.1) |
where, σij is a second order tensor known as stress tensor and its individual elements are the stress components.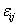 is another second order tensor known as strain tensor and its individual elements are the strain components. Cijkl is a fourth order tensor known as stiffness tensor. In the remaining section we will call it as stiffness matrix, as popularly known. The individual elements of this tensor are the stiffness coefficients for this linear stress-strain relationship. Thus, stress and strain tensor has ( is another second order tensor known as strain tensor and its individual elements are the strain components. Cijkl is a fourth order tensor known as stiffness tensor. In the remaining section we will call it as stiffness matrix, as popularly known. The individual elements of this tensor are the stiffness coefficients for this linear stress-strain relationship. Thus, stress and strain tensor has (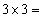 ) 9 components each and the stiffness tensor has ( ) 9 components each and the stiffness tensor has (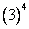 =) 81 independent elements. The individual elements =) 81 are referred by various names as elastic constants, moduli and stiffness coefficients. The reduction in the number of these elastic constants can be sought with the following symmetries. =) 81 independent elements. The individual elements =) 81 are referred by various names as elastic constants, moduli and stiffness coefficients. The reduction in the number of these elastic constants can be sought with the following symmetries.
Stress Symmetry:
The stress components are symmetric under this symmetry condition, that is, 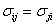 . Thus, there are six independent stress components. Hence, from Equation. (3.1) we write . Thus, there are six independent stress components. Hence, from Equation. (3.1) we write
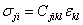 |
(3.2) |
Subtracting Equation (3.2) from Equation (3.1) leads to the following equation
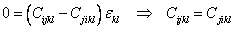 |
(3.3) |
There are six independent ways to express i and j taken together and still nine independent ways to express k and l taken together. Thus, with stress symmetry the number of independent elastic constants reduce to (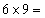 ) 54 from 81. ) 54 from 81.
Strain Symmetry:
The strain components are symmetric under this symmetry condition, that is, 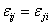 . Hence, from Equation (3.1) we write . Hence, from Equation (3.1) we write
Subtracting Equation (3.3) from Equation (3.2) we get the following equation
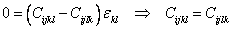 |
(3.4) |
It can be seen from Equation (3.4) that there are six independent ways of expressing i and j taken together when k and l are fixed. Similarly, there are six independent ways of expressing k and l taken together when i and j are fixed in Equation (3.4). Thus, there are 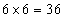 independent constants for this linear elastic material with stress and strain symmetry. independent constants for this linear elastic material with stress and strain symmetry.
With this reduced stress and strain components and reduced number of stiffness coefficients, we can write Hooke’s law in a contracted form as
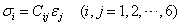 |
(3.5) |
where
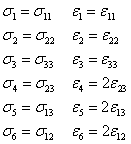 |
(3.6) |
Note: The shear strains are the engineering shear strains.
For Equation (3.5) to be solvable for strains in terms of stresses, the determinant of the stiffness matrix must be nonzero, that is 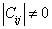 . .
The number of independent elastic constants can be reduced further, if there exists strain energy density function W, given as below.
|