In general, the viscosity of a fluid mainly depends on temperature. For liquids, the viscosity decreases with temperature and for gases, it increases with temperature. Sutherland's correlation is used to determine viscosity of gases as a function of temperature.
 |
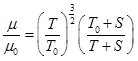(1.1.3) |
For air, the reference value of viscosity 
and S = 110K. In the case of liquids, the viscosity is approximated as below;
 |
(1.1.4) |
For water at 
.
5. Thermal Conductivity (k): It relates the rate of heat flow per unit area 
to the temperature gradient 
and is governed by Fourier Law of heat conduction i.e.
 |
(1.1.5) |
In SI system the unit and dimension of pressure can be written as, W/m.K and MLT-3θ-1, respectively. Thermal conductivity varies with temperature for liquids as well as gases in the same manner as that of viscosity. The reference value of thermal conductivity (k0) for water and air at reference temperature is taken as, 0.6 W/m.K and 0.025 W/m.K, respectively.
6. Coefficient of compressibility/Bulk modulus (Ev): It is the property of that fluid that represents the variation of density with pressure at constant temperature. Mathematically, it is represented as,
 |
(1.1.6) |
In terms of finite changes, it is approximated as,
 |
(1.1.7) |
It can be shown easily that Ev for an ideal gas at a temperature p is equal to its absolute pressure (N/m-2).
7. Coefficient of volume expansion (β): It is the property of that fluid that represents the variation of density with temperature at constant pressure. Mathematically, it is represented as,
 |
(1.1.8) |
In terms of finite changes, it is approximated as,
 |
(1.1.9) |
It can be shown easily that Ev for an ideal gas at a temperature T is equivalent to inverse of the absolute temperature.