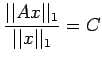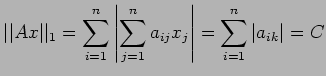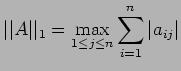: 4. The Elimination Method
: lec1
: 2. Norms of Vectors
In many problems we shall be concerned
at the same time with norms of vectors and matrices. It would seem
unwise if we use completely unrelated norms for the vectors and
matrices. It turns out to be convenient to have a matrix norm
'induced' by the vector norm. Thus we have:
If 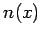 is a
vector norm satisfying the vector norm axioms, then for any matrix
A
Where the supremum is
over all non-zero vectors x, satisfies the matrix norm axioms and
is called the norm induced by n(x).
is a
vector norm satisfying the vector norm axioms, then for any matrix
A
Where the supremum is
over all non-zero vectors x, satisfies the matrix norm axioms and
is called the norm induced by n(x).
It is clean that, no matter
what 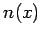 is, we have
It is not too difficult to
determine the matrix norms induced by our three basic vector
norms. These are given below:
is, we have
It is not too difficult to
determine the matrix norms induced by our three basic vector
norms. These are given below:
| Vector Norm |
Induced Matrix Norm |
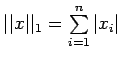 |
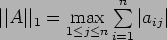 |
![$ \vert\vert x\vert\vert _2=\left[\sum\limits_{i=1}^n\vert x_i\vert^2\right]^{1/2}$](img63.png) |
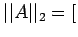 dominant eigen value of dominant eigen value of![$ A'A]^{1/2}$](img65.png) |
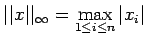 |
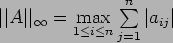 |
Here we give the proof of the first of the above results.
Use the vector norm
then
Changing the order of summation, we have
Let
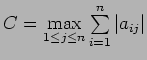 .
Then ............(1)
and thus
.
Then ............(1)
and thus
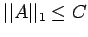
To show this is and equality, we demonstrate an x for which
Let k be the column index for which the maximum in (1) is
attained. Let 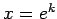 the
the 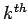 unit vector. Then
unit vector. Then 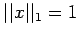 and
This process that for the vector norm
and
This process that for the vector norm 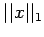 the induced matrix
norm is
the induced matrix
norm is



: 4. The Elimination Method
: lec1
: 2. Norms of Vectors
root
平成18年1月24日
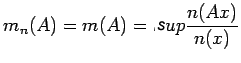
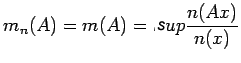
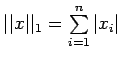
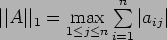
![$ \vert\vert x\vert\vert _2=\left[\sum\limits_{i=1}^n\vert x_i\vert^2\right]^{1/2}$](img63.png)
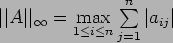
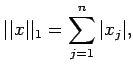
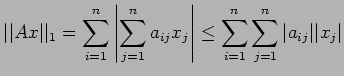
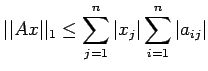
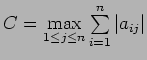 .
Then ............(1)
.
Then ............(1)