


: 3. Induced Norms:
: lec1
: 1. Some Notations:
Much work done on computers with vectors and matrices is
approximation mathematics, and it is necessary to be able to say
when one vector is near another, or when a vector is small, and
similarly for matrices. For this purpose the idem of norm is
introduced. In most cases, the norm of a 1-dimensional vector or
matrix is the absolute value of the number. We begin with three
vector norms in common use:
(i) Euclidean norm:
![$ \vert\vert x\vert\vert _2=[\sum\vert x_i\vert^2]^{1/2}]$](img36.png)
(ii) Maximum,Chebysher or sup norm:
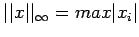
(iii) 1-norm:
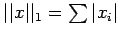
These three norms, which are non-negative functions on the
n-dimensional vector space 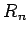 or
or 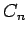 , satisfy the following
vector norm axioms:
, satisfy the following
vector norm axioms:
(V1)
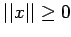 and
and 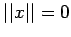 if and only if x = 0
if and only if x = 0
(V2)
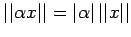 (Homogeneity)
(Homogeneity)
(V3)
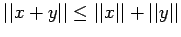 (Triangle
Inequality)
(Triangle
Inequality)
A Consequence of (V3) is
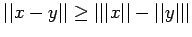 (Reverse Triangle
Inequality)
(Reverse Triangle
Inequality)
We now discuss some matrix norms:
i) Schur or Frobenius norm:
![$ \vert\vert A\vert\vert _F=[\sum\sum\vert a_{ij}\vert^2]^{1/2}$](img44.png)
ii) Max absolute row sum norm:
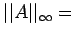 max
max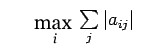
iii) Max absolute column sum norm:
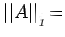 max
max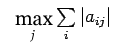
iv) 2-norm: 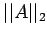 = [dominant eigen value of AA]
= [dominant eigen value of AA]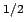
It can be verified that if these satisfy the matrix norm axioms
:
(M1)
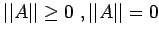 if and only if A =0
if and only if A =0
(M2)
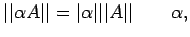 a scalar.
a scalar.
(M3)
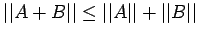
(M4)
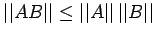
Example: Compute the 1,-2-,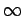 -, and Frobenious norms of the
matrix
-, and Frobenious norms of the
matrix



: 3. Induced Norms:
: lec1
: 1. Some Notations:
root
平成18年1月24日
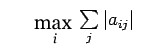
![\begin{displaymath}A=\left[%
\begin{array}{ccc}
5 & -5 & -7 \\
-4 & 2 & -4 \\
-7 & -4 & 5 \\
\end{array}%
\right]\end{displaymath}](img56.png)