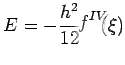The basic idea behind numerical
differentiation is very simple. If given the set of values
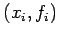
i=0,1,...,n, we determine the interpolating polynomial
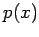
through these points. We then differentiate this polynomial
to obtain
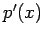
whose values for any
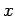
is taken as an
approximation to
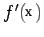
. Let us very briefly describe this
interpolating polynomial.
Let
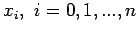
be
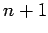
distinct points on an interval
I and let
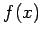
be a real valued function which takes on the
values
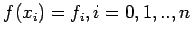
, at these n+1 points. To construct
a polynomial of degree not exceeding n which passes through the
n+1 points
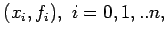
we use the method of
Lagrange. We begin by expressing the desired polynomial as

![]()
![]()
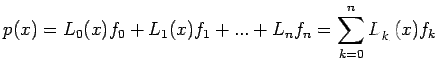
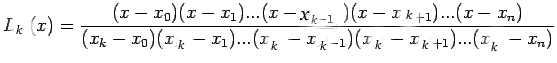
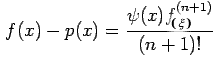
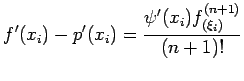
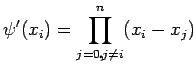
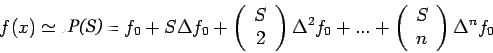 ..........(1)
..........(1)
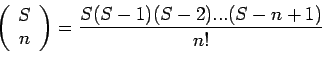
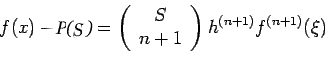 .
.
![\begin{displaymath}f'(x)\simeq\frac{1}{h}\frac{dP}{dS}=\frac{1}{h}[\Delta f_0+\f...
...in{array}{c}
S \\
n \\
\end{array}%
\right)\Delta^nf_0]\end{displaymath}](img467.png)
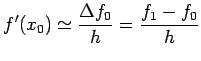
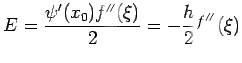
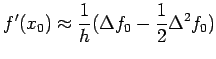
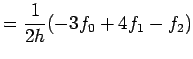
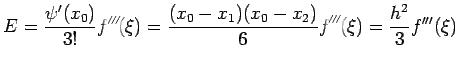
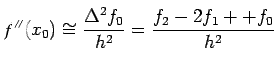
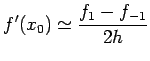
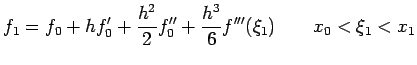
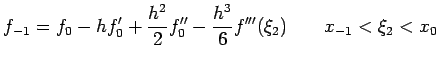
![$\displaystyle \frac{f_1-f_{-1}}{2h}=f'(x_0)+\frac{h^2}{12}[f'''(\xi_1)+f'''(\xi_2)]$](img484.png)
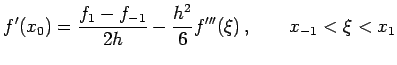
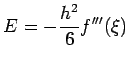
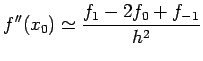 with error
with error