
Exercises:
- Prove the following:
a)
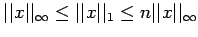
b)
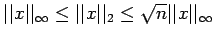
- Let A be a real non singular matrix of order n, and let
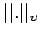 denote a vector norm on
denote a vector norm on 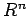 . Define
. Define
Show that 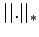 is a vector norm on
is a vector norm on 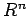 .
.
- Let
![$A(\alpha)=\left[%
\begin{array}{cc}
0.1\alpha & 0.1\alpha \\
1.0 & 1.5 \\
\end{array}%
\right]$](img7.png)
Determine 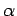 such that Cond
such that Cond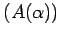 is minimised. Use
the maximum norm.
is minimised. Use
the maximum norm.
- Solve the following systems
-
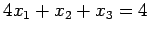
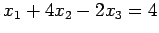
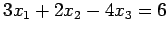
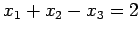
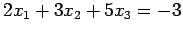
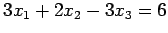
by Gauss elimination i) without pivoting and ii) with partial
pivoting.
- Find the Inverse of the matrix
by Gauss-Jordan method.
- The following system of equation is given
- Set up the Jacobi and Gauss-Seidel iterative schemes for the
solution and iterate three times starting with the initial vector
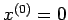 . Compare with the exact solution.
. Compare with the exact solution.
- The system of equations
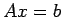 is to be solved iteratively
by
is to be solved iteratively
by
Suppose
![$A=\left[%
\begin{array}{cc}
1 & k \\
2k & 1 \\
\end{array}%
\right]$](img23.png) ,
,
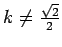 , k is real.
, k is real.
- Find a necessary and sufficient condition on k for
convergence of the Jacobi method.
- Consider the tridiagonal matrix given by
Show that A is nonsingular. Find a bound for
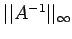 and
and 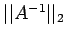 .
.
- Show using elimination that the following system does not
have a solution:
- For the system
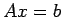 with
with
- Find det.(A) and
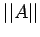 . Is A ill-Conditioned?
. Is A ill-Conditioned?
- For
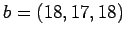 , the solution is
, the solution is 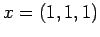 . Solve the
system for the vectors
. Solve the
system for the vectors 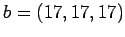 and
and
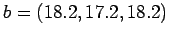 and
observe how the solution change.
and
observe how the solution change.

![$A(\alpha)=\left[%
\begin{array}{cc}
0.1\alpha & 0.1\alpha \\
1.0 & 1.5 \\
\end{array}%
\right]$](img7.png)
![\begin{displaymath}\left[%
\begin{array}{ccc}
1 & 2 & 1 \\
2 & 3 & -1 \\
2 & -1 & 3 \\
\end{array}%
\right]
\end{displaymath}](img16.png)
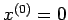 . Compare with the exact solution.
. Compare with the exact solution.
![$A=\left[%
\begin{array}{cc}
1 & k \\
2k & 1 \\
\end{array}%
\right]$](img23.png) ,
,
![\begin{displaymath}A=\left[%
\begin{array}{ccccc}
4 & 1 & & & \\
1 & 4 & 1...
... \\
& & 1 & 4 & 1 \\
& & & & 4 \\
\end{array}%
\right]\end{displaymath}](img25.png)
![\begin{displaymath}A=\left[%
\begin{array}{ccc}
5 & 6 & 7 \\
6 & 5 & 6 \\
7 & 5 & 6 \\
\end{array}%
\right]\end{displaymath}](img31.png)
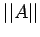 . Is A ill-Conditioned?
. Is A ill-Conditioned?
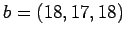 , the solution is
, the solution is 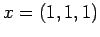 . Solve the
system for the vectors
. Solve the
system for the vectors 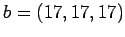 and
and
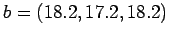 and
observe how the solution change.
and
observe how the solution change.