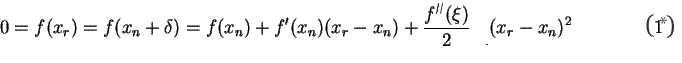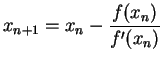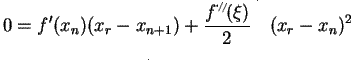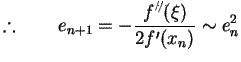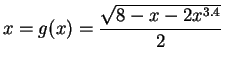Next: Fixed point Iteration: Up: Main Previous: Newton-Raphson Method:

Convergence of Newton-Raphson method:

Suppose $x_{r}$ is a root of $f(x)=0$ and $x_{n}$ is an estimate of $x_{r}$ s.t. $\vert x_{r}-x_{n}\vert=\delta << 1$. Then by Taylor series expansion we have,

for some between $x_{n}$ and $x_{r}$.
By Newton-Raphson method, we know that

$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}$$

i.e.

Using(2*) in (1*) we get

Say $$e_{n}=(x_{r}-x_{n}),\quad e_{n+1}=x_{r}-x_{n+1}$$

where $e_{n},\quad e_{n+1}$ denote the error in the solution at n$^{th}$ and (n+1)$^{th}$ iterations.

$$\Rightarrow e_{n+1}\quad \propto \quad e^{2}_{n}$$

$\therefore$ Newton Raphson Method is said to have quadratic convergence.

Note:
Alternatively, one can also prove the quadratic convergence of Newton-Raphson method based on the fixed - point theory. It is worth stating few comments on this approach as it is a more general approach covering most of the iteration schemes discussed earlier.

A Brief discussion on Fixed Point Iteration:
Suppose that we are given a function $f(x)=0\qquad\qquad\qquad \,\,\,(i)$
on an interval $[a,b]$ for which we need to find a root. Derive , from it, an equation of the form:

Any solution to (ii) is called a fixed point and it is a solution of (i). The function g(x) is called as "Iteration function".

Example:
Given $f(x)=2x^{3.4}+4x^{2}+x-8=0$, one may re-write it as:

$$x=g(x)=8-2x^{3.4}-4x^{2}$$

or , $$x=g(x)=\frac{\sqrt{8-x-2x^{3.4}}}{2}$$

or , $$x=g(x)=\{(8-x-4x^{2})/2\}^{1/3.4}$$

where g(x) denotes possible choice iteration function.