
Next: Convergence of Newton-Raphson Method:
Up: Main Previous: Convergence of secant Method:
Newton-Raphson Method:
Unlike the earlier methods, this method requires only one
appropriate starting point ![]() as an initial assumption of
the root of the function
as an initial assumption of
the root of the function ![]() . At
. At
![]() a tangent
to
a tangent
to ![]() is drawn. Equation of this tangent is given by
is drawn. Equation of this tangent is given by
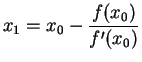
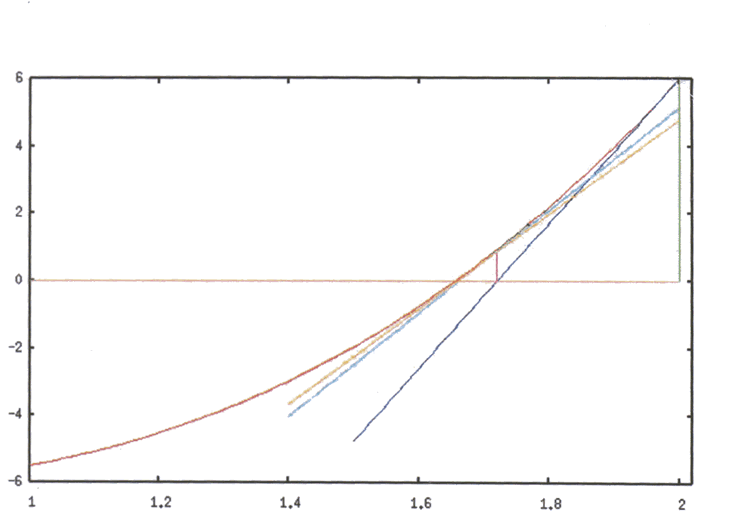
The various steps involved in calculating the root of ![]() by
Newton Raphson Method are described compactly in the algorithm
below.
by
Newton Raphson Method are described compactly in the algorithm
below.
Algorithm:
Given a continuously differentiable function
![]() and an initial approximation
and an initial approximation ![]() to the root of
to the root of ![]() , the steps involved in calculating an approximation
, the steps involved in calculating an approximation ![]() to the
root of
to the
root of ![]() s.t.
s.t.
![]() are:
are:
(1) Calculate
![]() and set
and set
![]()
(2) For n = 0,1,2... until convergence criteria is satisfied
,do:
Calculate
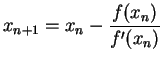
Remark (1): This method converges faster than the earlier methods. In fact the method converges at a quadratic rate. We will prove this later.
Remark (2): This method
can be derived directly by the Taylor expansion f(x) in the
neighbourhood of the root ![]() of
of ![]() . The starting
approximation
. The starting
approximation ![]() to
to ![]() is to be properly chosen so that
the first order Taylor series approximation of
is to be properly chosen so that
the first order Taylor series approximation of
![]() in the
neighbourhood of
in the
neighbourhood of ![]() leads to
leads to ![]() , an improved approximation
to
, an improved approximation
to ![]() . i.e
. i.e
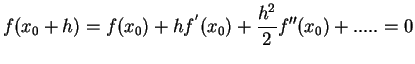
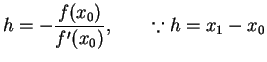
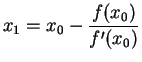
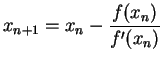
Remark(3) : One may also derive the above iteration formulation starting with the iteration formula for the secant method. In a way this may help one to visualize Newton-Raphson method as an improvement over the secant method. So, let us consider the iteration formula for the secant method i.e.
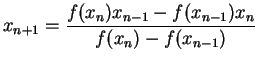
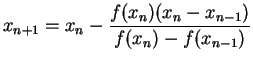
or , ![$\displaystyle x_{n+1}=x_{n}-\frac{f(x_{n})}{[f(x_{n})-f(x_{n-1})]/[x_{n}-x_{n-1}]}$](img202.png)
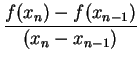 is
the slope of the secant to the curve
is
the slope of the secant to the curve 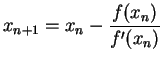
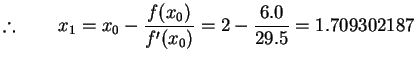
Since, ![]()
Therefore repeat the process.
Results are tabulated below:
Newton Rahpson Method
|
|||
Iteration no. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Say,
![]()
The results are tabulated below:
Newton Raphson Method
| Iteration no. |
|
||
| 0 | 0.5000000000 |
|
|
| 1 | 0.6934901476 |
|
0.0005313741 |
| 2 | 0.7013291121 |
|
0.0000003363 |
Exercise: Find the solutions accurate to within ![]() for the following problems using Newton-Raphson Method.
for the following problems using Newton-Raphson Method.
(1) ![]() for
for ![]() and
and ![]()
(2) ![]() for
for ![]() and
and ![]()