Next: Solutions Based on Power Up: Second Order and Higher Previous: Higher Order Equations with Contents
In the previous section, we have seen than a general solution of
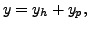
where
Case I.
![]()
We first assume that ![]() is not a root of the characteristic
equation, i.e.,
is not a root of the characteristic
equation, i.e.,
![]() Note that
Note that
![]() Therefore, let
us assume that a particular solution is of the form
Therefore, let
us assume that a particular solution is of the form
where
Since
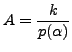 to obtain
to obtain
Thus,
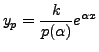 is a particular solution of
is a particular solution of
Modification Rule: If ![]() is a root of the characteristic
equation, i.e.,
is a root of the characteristic
equation, i.e.,
![]() with multiplicity
with multiplicity ![]() (i.e.,
(i.e.,
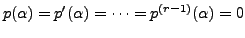 and
and
![]() ) then we take,
) then we take, ![]() of the form
of the form
and obtain the value of
So, we choose
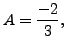 which gives a
particular solution as
which gives a
particular solution as
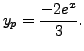
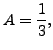 and thus a
particular solution is
and thus a
particular solution is
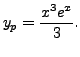
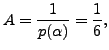 and hence a
particular solution is
and hence a
particular solution is
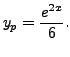
Case II.
![]()
We first assume that
![]() is not a root of the characteristic
equation, i.e.,
is not a root of the characteristic
equation, i.e.,
![]() Here, we assume that
Here, we assume that ![]() is of the form
is of the form
and then comparing the coefficients of
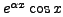 and
and
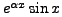 (why!) in
(why!) in
Modification Rule: If
![]() is a root of the
characteristic equation, i.e.,
is a root of the
characteristic equation, i.e.,
![]() with multiplicity
with multiplicity
![]() then we assume a particular solution as
then we assume a particular solution as
and then comparing the coefficients in
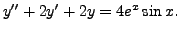
Thus, let us assume
![]() This
gives us
This
gives us
Comparing the coefficients of
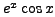 and
and
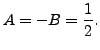 So,
a particular solution is
So,
a particular solution is
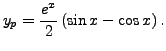
So, let
![]() Substituting
this in the given equation and comparing the coefficients of
Substituting
this in the given equation and comparing the coefficients of
![]() and
and ![]() on both sides,
we get
on both sides,
we get ![]() and
and
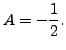 Thus,
a particular solution is
Thus,
a particular solution is
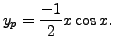
Case III.
![]()
Suppose
![]() Then we assume that
Then we assume that
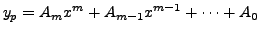
and then compare the coefficient of
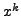 in
in
Modification Rule: If
![]() is a root of the
characteristic equation, i.e.,
is a root of the
characteristic equation, i.e., ![]() with multiplicity
with multiplicity
![]() then we assume a particular solution as
then we assume a particular solution as
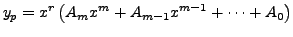
and then compare the coefficient of
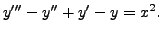
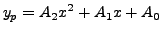
which on substitution in the given differential equation gives
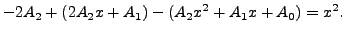
Comparing the coefficients of different powers of
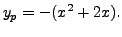
Finally, note that if 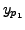 is a particular solution of
is a particular solution of
![]() and
and 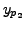 is a particular solution of
is a particular solution of
![]() then a particular solution of
then a particular solution of
is given by
In view of this, one can use method of undetermined coefficients for the cases, where
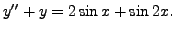
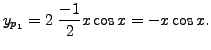
For the second problem, one can check that
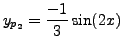 is a particular solution.
is a particular solution.
Thus, a particular solution of the given problem is
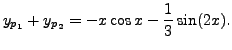
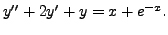
A K Lal 2007-09-12