Next: Linear Equations Up: Exact Equations Previous: Exact Equations Contents
On may occasions,
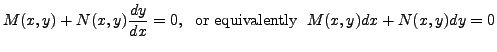
may not be exact. But the above equation may become exact, if we multiply it by a proper factor. For example, the equation
is not exact. But, if we multiply it with
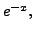 then the equation
reduces to
then the equation
reduces to
an exact equation. Such a factor (in this case,
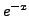 ) is called an INTEGRATING FACTOR
for the given equation. Formally
) is called an INTEGRATING FACTOR
for the given equation. Formally
is exact.
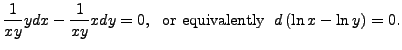
Thus, by definition,
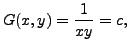 for some constant
for some constant
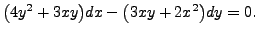
METHOD 1: Here the terms
![]() and
and
![]() are homogeneous functions of degree
are homogeneous functions of degree ![]() It may be checked that an integrating factor for the given differential equation is
It may be checked that an integrating factor for the given differential equation is
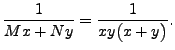
Hence, we need to solve the partial differential equations
for some real constant
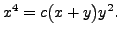
METHOD 2: Here the terms
![]() and
and
![]() are polynomial in
are polynomial in ![]() and
and ![]() Therefore,
we suppose that
Therefore,
we suppose that
![]() is an integrating factor for some
is an integrating factor for some
![]() We try to find this
We try to find this ![]() and
and ![]()
Multiplying the terms ![]() and
and ![]() with
with
![]() we get
we get
For the new equation to be exact, we need
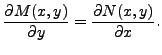 That is, the terms
That is, the terms
and
must be equal. Solving for
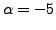 and
and
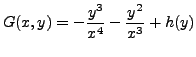
and
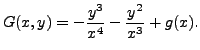
Thus, we need
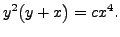
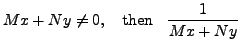
is an Integrating Factor.
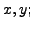 then
then
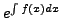 as an integrating factor,
if
as an integrating factor,
if
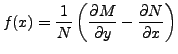 is a function of
is a function of 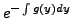 as an integrating factor,
if
as an integrating factor,
if
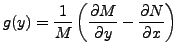 is a function of
is a function of
with
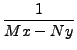 is
an integrating factor.
is
an integrating factor.
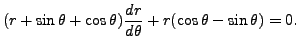
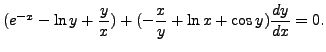
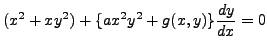
is exact.
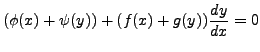
is exact.
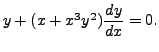
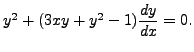
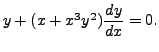
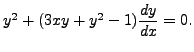
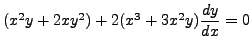 with
with 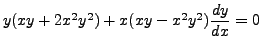 with
with A K Lal 2007-09-12