Next: Newton's Interpolation Formulae Up: Newton's Interpolation Formulae Previous: Averaging Operator Contents
Thus,
Thus
So we write,
Similarly,
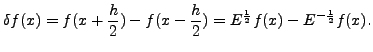
Thus,
Recall,
So, we have,
![$\displaystyle \framebox[1in][c]{$\mu^2\equiv \frac{\delta^2}{4}+1$} \;\; {\mbox{ or }}
\;\; \framebox[1in][c]{$\mu \equiv \sqrt{1+\frac{\delta^2}{4}}$}.$](img5019.png)
That is, the action of
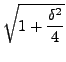 is same as that of
is same as that of ![$\displaystyle f(x+h)-f(x) = \frac{1}{2}\bigl[f(x+h)-2f(x)+f(x-h)
\bigr]+ \frac{1}{2}\bigl[f(x+h)-f(x-h)\bigr]$](img5022.png) |
|||
![$\displaystyle \frac{1}{2} \delta^2 (f(x)) +
\frac{1}{2}\bigl[f(x+h)-f(x-h)\bigr]$](img5023.png) |
![$\displaystyle \delta\left[\frac{1}{2}\left\{f(x+ \frac{h}{2})+
f(x-\frac{h}{2})\right\} \right] =
\frac{1}{2}\bigl[\{f(x+h)-f(x)\}+\{f(x)-f(x-h)\}\bigr]$](img5025.png) |
|||
![$\displaystyle \frac{1}{2}\left[f(x+h)-f(x-h)\right].$](img5026.png) |
![$\displaystyle \Delta f(x) = \left[\frac{1}{2}\delta^2+\delta
\mu\right]f(x),$](img5027.png)
i.e.,
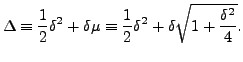
In view of the above discussion, we have the following table showing the relations between various difference operators:
| E | ||||
| E | E |
|
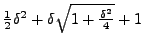
|
|
|
|
|
|||
|
|
|
|||
|
|
|
|
| 0 | 1 | 2 | 3 | 4 | |
| 93.0 | 96.5 | 100.0 | 103.5 | 107.0 | |
| 11.3 | 12.5 | 14.0 | 15.2 | 16.0 |
A K Lal 2007-09-12