Thevenin's Theorem

$v$ and $i$ will vary linearly in Fig.5.13.

Figure 5.13: Network (having sources also)

$$\Delta v \propto \Delta i$$

$$\frac{\Delta v}{\Delta i}=K$$

$$v=Ki+c$$

$$when\;v=0,\;i=\frac{-c}{K}$$

$$when\;i=0,\;v=c$$

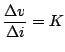This implies that voltage across load in figure 5.14 should be $v=Ki+c$

This implies: (see 5.15) $v=c-(-K)i$, that is, $v=c+Ki$.

Figure 5.14:

Figure 5.15: Getting an equivalent network

Hence, equivalent of network at terminal AB is shown in figure 5.16.

Figure 5.16: Equivalent Network

Here,
$V_{th}=C=$open circuit voltage
$R_{th}=\frac{open\;ckt\;voltage}{short\;ckt\;current}$

The two figures shown in figure 5.17 are equivalent. When the source inside the network is neglected (if voltage source, short ckted, if current source, open ckted)

Figure 5.17: Thevenin's Theorem: the two figures are equivalent

The same could be done with equivalent circuit.
hence, we get 5.18.

Figure 5.18: