Using NAND gates

Next: Boolean Expressions Up: Universality of certain gates Previous: Universality of certain gates Contents

Using NAND gates

NOT

**Figure 12.10:** Realizing a NOT gate using a NAND gate
$\includegraphics[width=2.5in]{lec15figs/10.eps}$

OR The following statements are called DeMorgan's Theorems and can be easily verified and extended for more than two variables.

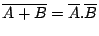$\displaystyle \overline{A+B}=\overline{A}.\overline{B}$			(12.1)
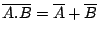$\displaystyle \overline{A.B}=\overline{A}+\overline{B}$			(12.2)

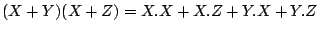$\displaystyle (X+Y)(X+Z)=X.X+X.Z+Y.X+Y.Z$	(12.3)
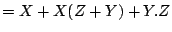$\displaystyle =X+X(Z+Y)+Y.Z$	(12.4)
In general: 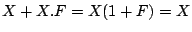$\displaystyle X+X.F=X(1+F)=X$	(12.5)
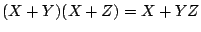Thus : $\displaystyle (X+Y)(X+Z)=X+YZ$	(12.6)

Now it is easy to see that 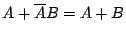$A+\overline{A}B=A+B$ , which can be checked from the truth table easily. The resulting realization of OR gate is shown in 12.11

**Figure 12.11:** Realization of OR gate by NAND gates
$\includegraphics[width=2.5in]{lec15figs/11.eps}$

AND gate

**Figure 12.12:** Realization of AND gate by NAND gates
$\includegraphics[width=2.5in]{lec15figs/12.eps}$

X-OR gate

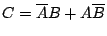$\displaystyle C=\overline{A}B+A\overline{B}$

(12.7)

Clearly, this can be implemented using AND, NOT and OR gates, and hence can be implemented using universal gates.

**Figure 12.13:** X-OR gate
$\includegraphics[width=2.5in]{lec15figs/13.eps}$

X-NOR gate

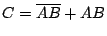$\displaystyle C=\overline{A}\overline{B}+AB$

(12.8)

Again, this can be implemented using AND, NOT and OR gates, and hence can be implemented using universal gates, i.e., NAND or NOR gates.

**Figure 12.14:** X-NOR gate
$\includegraphics[width=2.5in]{lec15figs/14.eps}$

Next: Boolean Expressions Up: Universality of certain gates Previous: Universality of certain gates Contents

ynsingh 2007-07-25