Constant voltage source

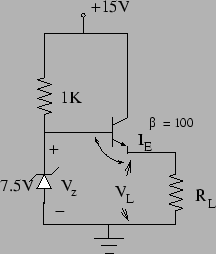
We can also have a constant voltage source whose output voltage would be more or less independent of the load . See the above figure. The output voltage would be as long as the transistor is not cutoff. The output voltage is therefore dependent upon .

We must ensure that the transistor is in the active region, whence, $V_{BE}=0.7$ volts. Therefore,

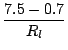$\displaystyle I_E$	$\displaystyle =$	$\displaystyle \frac{7.5-0.7}{R_l}$
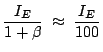$\displaystyle I_B$	$\displaystyle =$	$\displaystyle \frac{I_E}{1+\beta}\;\approx\;\frac{I_E}{100}$
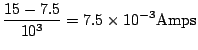$\displaystyle \mathrm{max}I_B$	$\displaystyle =$	$\displaystyle \frac{15-7.5}{10^3}=7.5\times 10^{-3}\mathrm{ Amps}$
$% latex2html id marker 9433 $\displaystyle \therefore \mathrm{ max}I_E$$	$\displaystyle =$	$\displaystyle 100 \times 7.5 \mathrm{ Amps }=\;0.75 \mathrm{ Amps}$
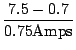$\displaystyle \Rightarrow\quad\mathrm{min }R_L$	$\displaystyle =$	$\displaystyle \frac{7.5-0.7}{0.75\mathrm{ Amps}}$
	$\displaystyle =$	$\displaystyle 9.07\mathrm{ Amps}$

Therefore, the above circuit works as a constant voltage source for $R_L>9.07\Omega$ .