CE Characteristics

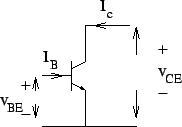
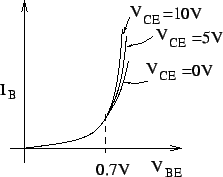
We have two independent variables here $I_B$ and $V_{CE}$. For different value of $V_{CE}$, the input characteristics $I_B$ as a function of $V{BE}$ is as follows.

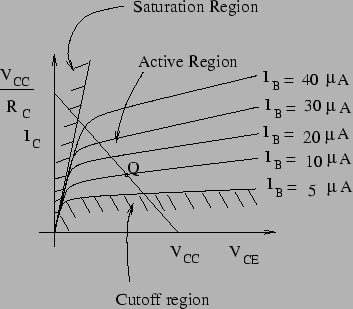
Similarly, for different values of $I_B$, the $I_C$ vs. $V_{CE}$ characteristic is shown below. The line passing through $(0,\frac{V_{CC}}{R_C})$ and $(V_{CC},0)$ is known as the load line and its intersection with the $I_C-V_{CE}$ curve determines the quiscent point or operating point Q. Note that in the active region, $I_C$ is almost independent of $V_{CE}$ (i.e. nearly constant) and depends mostly on $I_B$. The ratio $\frac{I_C}{I_B}$ is a constant for the active region and is known as $\beta$.

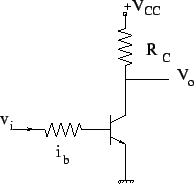
In the common emitter circuit shown above,

$$V_{CC}-I_CR_C = V_{CE}$$

$$I_C = -V_{CE}\times\frac{1}{R_C}+\frac{V_{CC}}{R_C}$$

The above is the equation of the load line. Q is the operating point for $I_B=10\mu$A. In the active region, $V_{BE}$ is approximately 0.7 V.

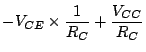For the cutoff region, $I_B=0$ and $V_{BE}<0.7$ V.

In the saturation region, $V_{CE}<0.2$V and $\frac{I_C}{I_B}=\beta$.

We will denote the operating point by $V_{CEQ}$ and $I_{CEQ}$.

The fact that in the active region, variations in $I_B$ result in proportional varitions in $I_C$ and hence $V_{CE}$ forms thefundamental principle of amplifier. For the trabsistor to remain in the active region throughout this variation, variations in $I_B$ should be maximum $\pm{}5\mu$A.

In the CE configuration above, with the change in temperature, $\beta$ changes and hence, so does Q. $\beta$ is an increasing function of T and therefore as T increases, $I_c$ increases causing further heating of the transistor and thereby further increasing $\beta$. This is known as thermal runaway. To avoid this, we stabilize the circuit my introducing an emitter resistance.

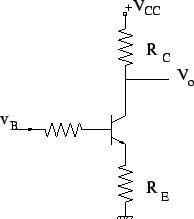
Now, as T increases, $\beta$ increases and so does $I_C$. This increases $I_E$ and therefore reduces $I_B$ as the base voltage increases. This decrease in $I_b$ resluts in decrease of $I_C$, thereby compensating the effect of temperature and stablization of the operating point.