| |
Example 13 :
Obtain an expression for the potential at a distance 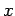 from a line charge distribution with a linear charge density from a line charge distribution with a linear charge density 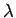 . .
Solution
The electric field due to the charge distribution at a point P located at a distance 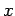 is is
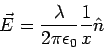
where 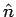 is along the perpendicular from the point P to the line charge, as shown (the direction is opposite if line charge density is negative). The potential difference between the point is along the perpendicular from the point P to the line charge, as shown (the direction is opposite if line charge density is negative). The potential difference between the point 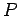 and a reference point and a reference point 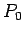 is obtained by calculating the value of the integral is obtained by calculating the value of the integral 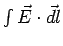 from the point from the point 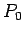 to the point to the point 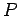 . As the integral is independent of path, we calculate it along the path . As the integral is independent of path, we calculate it along the path 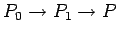 , as shown. The contribution to the integral from the path , as shown. The contribution to the integral from the path 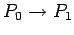 is zero as along this path is zero as along this path 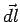 is perpendicular to is perpendicular to 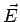 . Along the path . Along the path 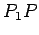 , the directions of , the directions of 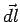 and and 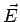 are parallel. are parallel.
|