| |
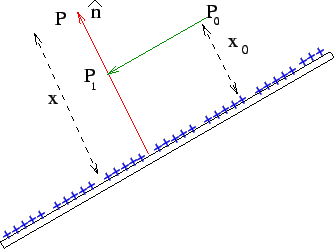
Hence, if the perpendicular distance of 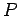 from the line charge is denoted by from the line charge is denoted by 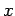
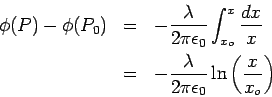
 Click here for Animation Click here for Animation
One can see that taking 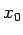 to be infinite will make the integral diverge. In this case, it it is convenient to take the zero of the potential to be at unit distance from the line ( to be infinite will make the integral diverge. In this case, it it is convenient to take the zero of the potential to be at unit distance from the line ( 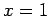 ). With this choice the potential at a distance ). With this choice the potential at a distance 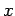 from the line is from the line is
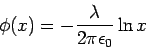
|