 |
Example 18 :
Determine the equipotential surface of an infinite line charge carrying a positive charge density 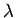 . .
Solution :
Let the line charge be along the z- axis. The potential due to a line charge at a point P is given by
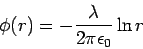
where 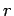 is the distance of the point P from the line charge. Since the line charge along the z-axis, is the distance of the point P from the line charge. Since the line charge along the z-axis, 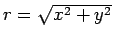 so that so that
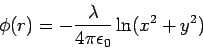
The surface
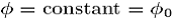 is given by is given by
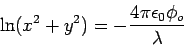
|