 |
Consider a spherical conductor of radius 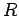 carrying a charge carrying a charge 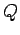 . The potential of the sphere is given by . The potential of the sphere is given by
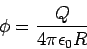
The potential of the conductor is proportional to the charge it contains. This linear relationship is true in general, independent of the shape of the conductor,
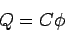
The constant of proportionality 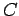 is called the capacitance of the conductor. For the conducting sphere the capacitance is is called the capacitance of the conductor. For the conducting sphere the capacitance is 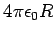 . . |