 |
The electric field at a distance 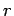 from the centre is calculated by using the Gaussian surface shown. The fileld is radial and is given by from the centre is calculated by using the Gaussian surface shown. The fileld is radial and is given by |
| |
|
| |
The voltage drop between the shells is obtained by integrating the electric field along a radial path (the electric field being conservative, the path of integration is chosen as per our convenience) from the negative plate to the positrive plate. |
| |
|
| |
The capacitance is |
| |
|
| |
Cylindrical Conductor : |
| |
A cylindrical capacitor consists of two long coaxial conducting cylinders of length 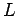 and radii and radii 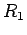 and and 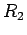 . The electric field in the space between the cylinders may be calculated by Gauss Law, using a pillbox in the shape of a short coaxial cylinder of length . The electric field in the space between the cylinders may be calculated by Gauss Law, using a pillbox in the shape of a short coaxial cylinder of length 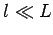 and radius and radius 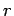 . Neglecting edge effects, the field is in the radial direction and depends only on the distance . Neglecting edge effects, the field is in the radial direction and depends only on the distance 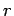 from the axis. from the axis. |
| |
|
|