 |
Example 20 :
A hemispherical bowl of radius 1 lies with its base on the x-y plane and the origin at the centre of the circular base. Calculate the surface integral of the vector field 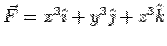 in the hemisphere and verify the divergence theorem. in the hemisphere and verify the divergence theorem.
Solution :
The divergence of 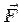 is easily calculated is easily calculated
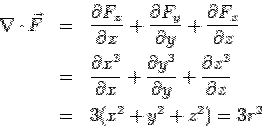
where 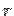 is the distance from origin. The volume integral over the hemisphere is conveniently calculated in spherical polar using the violume element is the distance from origin. The volume integral over the hemisphere is conveniently calculated in spherical polar using the violume element 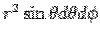 . Since it is a hemisphere with . Since it is a hemisphere with 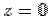 as the base, the range of as the base, the range of 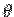 is is 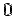 to to 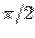 . . |