 |
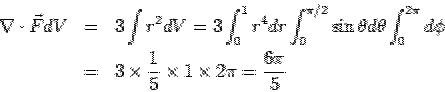
The surface integrals are calculated conveniently in spherical polar. There is no contribution to the flux from the base because the outward normal points in the 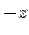 direction but the z-component of the field is zero because the base of the hemisphere is direction but the z-component of the field is zero because the base of the hemisphere is 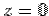 . .
In order to calculate the flux from the curved face we need to express the force field and the unit vectors in spherical polar coordinates. Using the tranformation properties given earlier and observing that we only require the radial component of the vector field since the area element is radially directed. Using 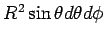 as the area element, a bit of laborious algebra gives as the area element, a bit of laborious algebra gives
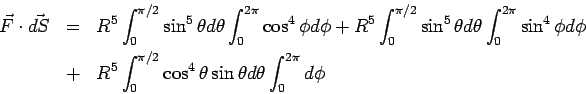
Using 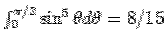 and and 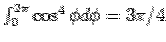 , the above integral can be seen to give the correct result. , the above integral can be seen to give the correct result. |