| |
Express unit vectors of spherical coordinate system in terms of unit vectors of cartesian system. |
| |
From the point P drop a perpendicular on to the x-y plane. Denote 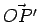 by by 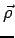 . The figure below shows the unit vectors in both the systems. By triangle law of vector addition, . The figure below shows the unit vectors in both the systems. By triangle law of vector addition, |
| |
However, 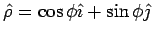 . Substituting this in the expression for . Substituting this in the expression for 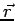 , we get on dividing both sides by the magnitude of , we get on dividing both sides by the magnitude of 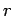 |